【理論】令和6年 (下期) 問8|交流電圧源の直列回路における合成電圧の最大値と位相の計算問題
図のように,二つの正弦波交流電圧源 \( e_1 \) [V],\( e_2 \) [V] が直列に接続されている回路において,
合成電圧 \( v \) [V] の最大値は \( e_1 \) の最大値の \( \fbox{(ア)} \) 倍となり,その位相は \( e_1 \) を基準として \( \fbox{(イ)} \) [rad] の \( \fbox{(ウ)} \) となる。
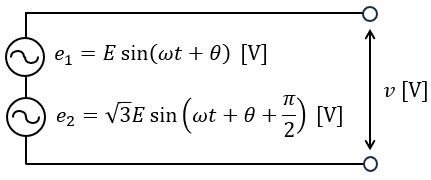
\[ \begin{array}{cccc} & (ア) & (イ) & (ウ) \\ \hline (1) & \displaystyle \frac{1}{2} & \displaystyle \frac{\pi}{3} & \text{進み} \\ \hline (2) & 1 + \sqrt{3} & \displaystyle \frac{\pi}{6} & \text{遅れ} \\ \hline (3) & 2 & \displaystyle \frac{\pi}{3} & \text{進み} \\ \hline (4) & \sqrt{3} & \displaystyle \frac{\pi}{6} & \text{遅れ} \\ \hline (5) & 2 & \displaystyle \frac{2\pi}{3} & \text{進み} \\ \hline \end{array} \]
合格への方程式
問題と基本概念
今回の問題
図のように,二つの正弦波交流電圧源 \( e_1 \, \mathrm{[V]} \),\( e_2 \, \mathrm{[V]} \) が直列に接続されている回路において,合成電圧 \( v \, \mathrm{[V]} \) の最大値は \( e_1 \) の最大値の (ア) 倍となり,その位相は \( e_1 \) を基準として (イ)[rad] の (ウ) となる。
→ 横スクロールして下さい →
\[ \begin{array}{cccc} & (ア) & (イ) & (ウ) \\ \hline (1) & \displaystyle \frac{1}{2} & \displaystyle \frac{\pi}{3} & \text{進み} \\ \hline (2) & 1 + \sqrt{3} & \displaystyle \frac{\pi}{6} & \text{遅れ} \\ \hline (3) & 2 & \displaystyle \frac{\pi}{3} & \text{進み} \\ \hline (4) & \sqrt{3} & \displaystyle \frac{\pi}{6} & \text{遅れ} \\ \hline (5) & 2 & \displaystyle \frac{2\pi}{3} & \text{進み} \\ \hline \end{array} \]
この問題のポイント
重要なポイント
- 正弦波交流電圧の合成はベクトル演算で行う
- 位相と振幅が異なる交流電圧の合成を理解する
- ベクトル図を正確に描けるかがカギ
- 三角関数の知識(特に30°、60°の値)が必要
交流電圧の合成とは
直流の場合、電圧の合成は単純な足し算ですが、交流の場合は話が違います。交流では電圧の大きさだけでなく、位相(タイミング)も考慮する必要があります。
身近な例で考えてみよう
これは二人で重いものを持ち上げる時に似ています。二人が同じタイミングで力を入れれば(位相が同じ)力は単純に足し算されますが、タイミングがずれていると(位相が異なる)効果的に力を合わせることができません。交流電圧でも同じことが起こります。
問題を解くための準備
この問題を解くには以下の知識が必要です:
- 正弦波交流の表現方法:瞬時値、実効値、最大値
- ベクトル表示:複素平面での表現
- ベクトルの合成:平行四辺形の法則
- 三角関数の値:特に30°、60°、90°
よくある間違い
- 交流電圧を直流のように単純に足し算してしまう
- 位相差を度数とラジアンで混同する
- ベクトル図の向きを間違える
- 最大値と実効値を混同する
正弦波交流の基礎知識
正弦波交流の数学的表現
電圧や電流の実効値が \( V \, \mathrm{[V]} \) 及び \( I \, \mathrm{[A]} \),角周波数が \( \omega \, \mathrm{[rad/s]} \),電圧及び電流の初期位相が \( \theta \, \mathrm{[rad]} \) 及び \( \phi \, \mathrm{[rad]} \) の正弦波交流があるとき,それぞれの瞬時値は:
三相交流正弦波を可視化
電験三種 理論基礎 | 三相交流正弦波(リアルタイム位相差調整)シミュレーター→ 横スクロールして下さい →
\[ \begin{aligned} v &= \sqrt{2}V \sin(\omega t + \theta) \, \mathrm{[V]} \\[10pt] i &= \sqrt{2}I \sin(\omega t + \phi) \, \mathrm{[A]} \end{aligned} \]重要な関係式
- 最大値 = \( \sqrt{2} \times \) 実効値
- 実効値 = \( \frac{1}{\sqrt{2}} \times \) 最大値
- \( \sqrt{2} \approx 1.414 \)
ベクトル表示(フェーザ表示)
正弦波交流は回転するベクトルとして表現できます。これをフェーザと呼びます。
自由にベクトルを描画できます。加算減算も可能
電験三種 数学基礎 | ベクトル(交流回路図)インタラクティブ解説ツールベクトル表示の利点
- 複雑な三角関数の計算をベクトル演算に置き換えられる
- 位相関係が視覚的に分かりやすい
- 回路解析が簡単になる
複素数表示
ベクトルは複素数として表現することもできます:
\[ \dot{V} = V e^{j\theta} = V(\cos\theta + j\sin\theta) \]ここで:
- \( V \):振幅(大きさ)
- \( \theta \):位相角
- \( j \):虚数単位(\( j^2 = -1 \))
位相差の考え方
位相差の例
- 同相(位相差0°):二つの波形が同じタイミングで変化
- 逆相(位相差180°):片方が最大の時、もう片方が最小
- 直交(位相差90°):片方が最大の時、もう片方がゼロ
| 位相関係 | 位相差(度) | 位相差(ラジアン) | 合成結果 |
|---|---|---|---|
| 同相 | 0° | 0 | 振幅が足し算 |
| 直交 | 90° | \( \frac{\pi}{2} \) | ピタゴラスの定理 |
| 逆相 | 180° | \( \pi \) | 振幅が引き算 |
角度の単位変換
度とラジアンの変換
- \( 180° = \pi \, \mathrm{rad} \)
- \( 90° = \frac{\pi}{2} \, \mathrm{rad} \)
- \( 60° = \frac{\pi}{3} \, \mathrm{rad} \)
- \( 30° = \frac{\pi}{6} \, \mathrm{rad} \)
三角関数の重要な値
| 角度 | sin | cos | tan |
|---|---|---|---|
| 0° | 0 | 1 | 0 |
| 30° | \( \frac{1}{2} \) | \( \frac{\sqrt{3}}{2} \) | \( \frac{1}{\sqrt{3}} \) |
| 60° | \( \frac{\sqrt{3}}{2} \) | \( \frac{1}{2} \) | \( \sqrt{3} \) |
| 90° | 1 | 0 | ∞ |
覚え方のコツ
30°、60°の三角関数の値は「1、2、3の平方根」で覚えられます。sinは「1、2、3」の順、cosは「3、2、1」の順に \( \frac{\sqrt{n}}{2} \) となります。
ベクトル図を使った解き方
問題の回路と条件の整理
この問題では、図から以下の条件が読み取れます:
- \( e_1 \) と \( e_2 \) は直列に接続されている
- \( e_1 \) を基準(位相0°)として考える
- \( e_2 \) は \( e_1 \) に対して特定の位相差を持つ
- \( e_2 \) の振幅は \( e_1 \) の \( \sqrt{3} \) 倍
ベクトル図の描き方
直列接続された交流電圧源の合成は、ベクトルの足し算で求められます。
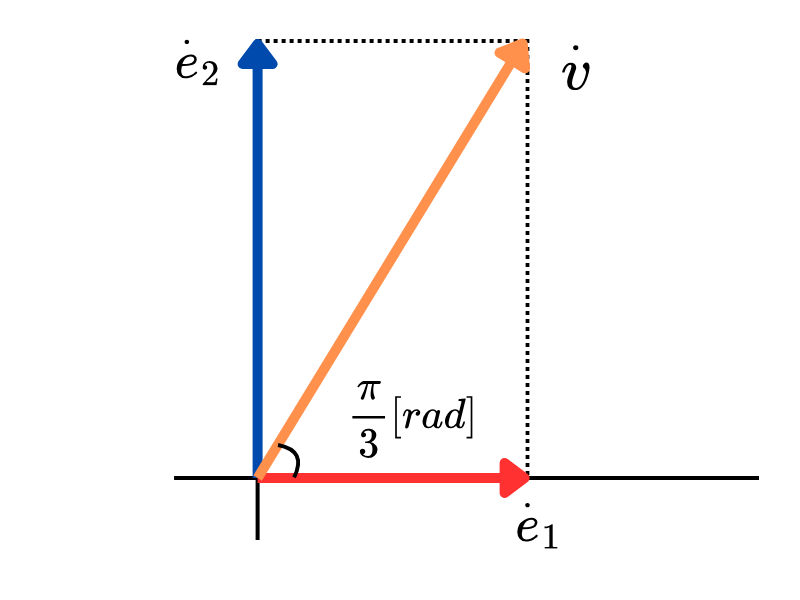
ベクトル図から読み取れること
- \( e_1 \):基準ベクトル(水平右向き)
- \( e_2 \):\( e_1 \) の \( \sqrt{3} \) 倍の長さ、60°進み位相
- \( v \):\( e_1 \) と \( e_2 \) のベクトル合成
計算による解法
ステップ1:各ベクトルの成分表示
\( e_1 \) の振幅を \( E \) とすると:
- \( \dot{e_1} = E \angle 0° = E + j0 \)
- \( \dot{e_2} = \sqrt{3}E \angle 90° = \sqrt{3}E(\cos 90° + j\sin 90°) \)
ステップ2:\( e_2 \) の成分計算
\[ \dot{e_2} = \sqrt{3}E(0 + j \cdot 1) = j\sqrt{3}E \]ステップ3:合成電圧の計算
\[ \begin{aligned} \dot{v} &= \dot{e_1} + \dot{e_2} \\[10pt] &= E + j0 + j\sqrt{3}E \\[10pt] &= E + j\sqrt{3}E \\[10pt] &= E(1 + j\sqrt{3}) \end{aligned} \]ステップ4:合成電圧の大きさ
\[ |\dot{v}| = E\sqrt{1^2 + (\sqrt{3})^2} = E\sqrt{1 + 3} = E\sqrt{4} = 2E \]ステップ5:合成電圧の位相
\[ \angle \dot{v} = \arctan\left(\frac{\sqrt{3}}{1}\right) = \arctan(\sqrt{3}) = 60° = \frac{\pi}{3} \, \mathrm{rad} \]幾何学的解法(より簡単な方法)
ベクトル図を見ると、これは特別な三角形になっています。
特別な三角形の性質を利用
角度が30°-60°-90°の直角三角形では、辺の比が 1 : \( \sqrt{3} \) : 2 となります。
様々な三角比を確認できます。
電験三種 数学基礎 | 三角比(sin・cos・tan)インタラクティブ解説ツール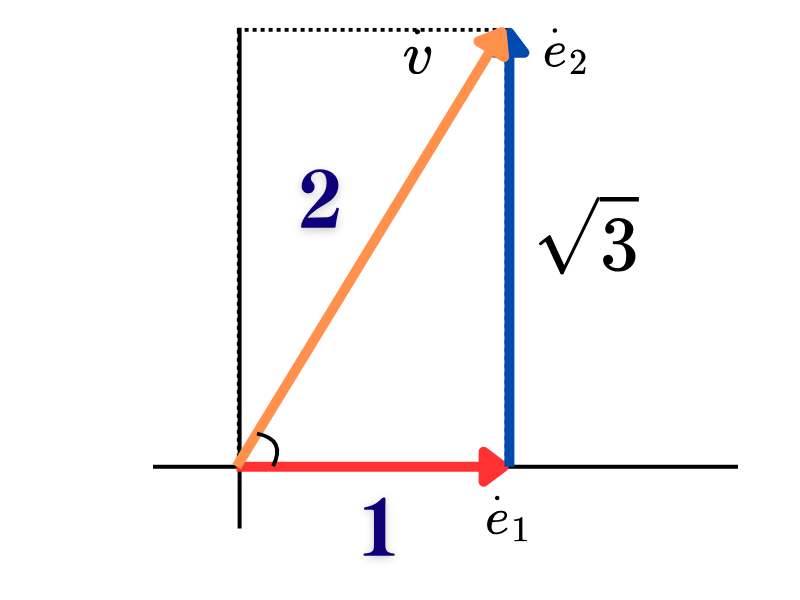
(ア)合成電圧の大きさ
ベクトル図から、合成ベクトルの大きさは \( e_1 \) の 2倍 になることが分かります。
(イ)合成電圧の位相
合成ベクトルは \( e_1 \) を基準として \( \frac{\pi}{3} \, \mathrm{rad} \)(60°の半分の30°)進んでいます。
(ウ)位相の進み・遅れ
合成ベクトルは \( e_1 \) よりも反時計回り方向にあるので、進み位相です。
進み・遅れの判定方法
- 進み:基準より反時計回り方向(正の角度)
- 遅れ:基準より時計回り方向(負の角度)
答え:(3) \( 2 \)、\( \frac{\pi}{3} \)、進み
応用問題と発展的な考え方
類似問題のパターン
交流電圧の合成問題には以下のような様々なパターンがあります:
パターン1:異なる位相差
30°、45°、120°など、異なる位相差での合成問題があります。それぞれ異なる計算テクニックが必要です。
パターン2:3つ以上の電圧源
3相交流系統では、120°ずつ位相差のある3つの電圧源を扱います。
パターン3:インピーダンスとの組み合わせ
抵抗、コイル、コンデンサが混在する回路での電圧分解問題もあります。
実際の応用分野
→ 横スクロールして下さい →
| 応用分野 | 具体例 | 重要性 |
|---|---|---|
| 3相電力系統 | 送電線の不平衡解析 | 電力品質の維持 |
| 変圧器設計 | 巻線間の位相関係 | 効率的な電力変換 |
| 電動機制御 | 回転磁界の生成 | 滑らかな回転制御 |
| フィルタ回路 | 高調波成分の合成 | ノイズ除去 |
| 通信回路 | 信号の変調・復調 | 情報の正確な伝送 |
より高度な解析手法
対称座標法
3相不平衡系統の解析では、対称座標法という特別な手法を使います。正相、逆相、零相の3つの成分に分解して考えます。
高調波解析
実際の交流波形には基本波以外に高調波成分が含まれます。これらの合成を考える際も、同様のベクトル演算が使われます。
フーリエ解析との関連
複雑な波形は正弦波の合成として表現できます(フーリエ級数)。各正弦波成分をベクトルとして扱い、それらの合成を考えることで、複雑な現象も理解できます。
計算上のコツとポイント
効率的な解法の選択
- 特別な角度の場合:30°、45°、60°、90°などは三角関数の値を暗記
- 対称性の利用:同じ振幅や等間隔の位相差では対称性を活用
- ベクトル図の活用:複雑な計算より視覚的理解を優先
- 複素数表示:計算が複雑な場合は複素数演算を活用
実験での確認方法
理論計算の結果は、オシロスコープを使った実験で確認できます:
- 関数発生器で位相差のある2つの正弦波を生成
- 加算回路で電圧を合成
- オシロスコープで各波形と合成波形を同時観測
- リサージュ図形で位相関係を確認
実験上の注意点
- 回路の寄生容量や寄生インダクタンスが高周波で影響
- 測定器の入力インピーダンスによる負荷効果
- 接地の取り方による測定誤差
- 温度変化による機器特性の変動
発展学習への道筋
この基本的な交流合成の理解から、以下の発展的な内容へ進むことができます:
学習の発展方向
- 回路解析:キルヒホッフの法則の交流への適用
- 電力計算:有効電力、無効電力、皮相電力
- 共振回路:RLC回路の周波数特性
- 伝送線路理論:高周波での波動現象
- 電気機器:回転機の原理と特性
学習のポイント
まずは基本的なベクトル演算をしっかりマスターすることが重要です。複雑な問題も、結局は基本的なベクトルの足し算の組み合わせです。視覚的な理解と数学的な計算の両方をバランスよく身につけましょう。
🔍 ワンポイントアドバイス: 交流電圧の合成問題は「ベクトル図を正確に描く」ことが最重要です。数式だけで解こうとせず、必ずベクトル図を描いて視覚的に理解しましょう。特に30°、60°、90°の特別な角度では、三角関数の値を覚えておくと計算が格段に速くなります。また、進み・遅れの判定は「反時計回りが進み」と覚えておけば間違いません。この基本をマスターすれば、より複雑な3相交流や回路解析の問題にも対応できるようになります。
さあ、今度は交流の問題やで!直流とは違って、交流は位相っていう厄介なヤツが出てくるんや。
でも大丈夫、一歩ずつ理解していけば絶対解けるから安心してや。まずは問題を見てみよう!
二つの正弦波交流電圧源 \( e_1 \) と \( e_2 \) が直列に繋がってるな。そして合成電圧 \( v \) の最大値と位相を求める問題や。何がポイントになると思う?
まずは問題の構成を整理いたします:
【与えられた情報】
・\( e_1 = E \sin(\omega t + \theta) \, \mathrm{[V]} \)
・\( e_2 = \sqrt{3}E \sin(\omega t + \theta + \frac{\pi}{2}) \, \mathrm{[V]} \)
・二つの電圧源が直列接続されている
【求めるもの】
・合成電圧 \( v \) の最大値(\( e_1 \) の最大値の何倍か)
・合成電圧 \( v \) の位相(\( e_1 \) 基準で何ラジアン進みか遅れか)
【解法のポイント】
交流の合成は、ベクトル図を使って視覚的に解くのが最も分かりやすい方法です。各電圧源をベクトルとして表現し、ベクトルの合成として解いていきます。
そうや!交流の合成はベクトル図が一番や。でもその前に、交流の基本を確認しとこか。
正弦波交流 \( v = V_m \sin(\omega t + \theta) \) っていう式があるやろ?この \( V_m \) が最大値で、\( \theta \) が初期位相なんや。まずはこの基本をしっかり理解してから進もうな。
三相交流正弦波を可視化
電験三種 理論基礎 | 三相交流正弦波(リアルタイム位相差調整)シミュレーター【交流電圧の基本式の理解】
一般的な正弦波交流電圧は以下の形で表されます:
→ 横スクロールして下さい →
\[ v(t) = V_m \sin(\omega t + \theta) \]ここで:
・\( V_m \):最大値(振幅)\( \mathrm{[V]} \)
・\( \omega \):角周波数 \( \mathrm{[rad/s]} \)
・\( t \):時間 \( \mathrm{[s]} \)
・\( \theta \):初期位相 \( \mathrm{[rad]} \)
【本問題での各電圧源の解析】
\( e_1 = E \sin(\omega t + \theta) \) → 最大値:\( E \)、初期位相:\( \theta \)
\( e_2 = \sqrt{3}E \sin(\omega t + \theta + \frac{\pi}{2}) \) → 最大値:\( \sqrt{3}E \)、初期位相:\( \theta + \frac{\pi}{2} \)
つまり \( e_2 \) は \( e_1 \) よりも \( \frac{\pi}{2} \) だけ位相が進んでいます。
よし、基本は大丈夫やな!そしたら次に、ベクトル図の描き方を教えたるで。
交流電圧はベクトルとして表現できるんや。長さが最大値、角度が位相を表すんやで。\( e_1 \) を基準(水平右向き)にして、\( e_2 \) と合成電圧 \( v \) を描いてみよう。
自由にベクトルを描画できます。加算減算も可能
電験三種 数学基礎 | ベクトル(交流回路図)インタラクティブ解説ツール【ベクトル図の基本的な描き方】
交流電圧をベクトルで表現する場合:
・ベクトルの長さ = 電圧の最大値
・ベクトルの角度 = 位相
・回転方向は反時計回りが正(進み位相)
【\( e_1 \) 基準のベクトル設定】
1. \( e_1 \) を基準として水平右向き(0°)に描きます
・長さ:\( E \)
・角度:0°(基準)
2. \( e_2 \) は \( e_1 \) より \( \frac{\pi}{2} \) 進んでいるので:
・長さ:\( \sqrt{3}E \)
・角度:\( \frac{\pi}{2} \)(90°上向き)
【合成ベクトルの考え方】
直列接続では電圧が加算されるので、\( \vec{v} = \vec{e_1} + \vec{e_2} \) となります。
これはベクトルの頭尻法則で求めることができます。
ええ感じや!そしたら実際にベクトル図を描いてみよう。

ほら、こんな感じや!\( e_1 \) を赤い矢印で右向きに、\( e_2 \) を青い矢印で上向きに描いてる。そして合成電圧 \( v \) がオレンジの矢印やな。この図から何が分かるかな?
【ベクトル図の読み取り】
図から以下のことが読み取れます:
1. 各ベクトルの特徴
・\( \vec{e_1} \)(赤):長さ 1、水平右向き(0°)
・\( \vec{e_2} \)(青):長さ \( \sqrt{3} \)、垂直上向き(90°)
・\( \vec{v} \)(オレンジ):合成ベクトル
2. 直角三角形の形成
\( \vec{e_1} \) と \( \vec{e_2} \) が垂直に配置されているため、直角三角形が形成されています。
・底辺:\( |\vec{e_1}| = 1 \)(\( E \) を1として正規化)
・高さ:\( |\vec{e_2}| = \sqrt{3} \)
・斜辺:\( |\vec{v}| = ? \)(これを求める)
3. 位相関係
合成ベクトル \( \vec{v} \) は \( \vec{e_1} \) を基準として、ある角度だけ進み位相になっています。
そうそう!直角三角形になってるのがポイントやな。そしたら三角比を使って計算してみよう。
底辺が 1、高さが \( \sqrt{3} \) の直角三角形やから、ピタゴラスの定理で斜辺の長さが求められるで。そして角度は逆三角関数やな。計算してみよか!
様々な三角比を確認できます。
電験三種 数学基礎 | 三角比(sin・cos・tan)インタラクティブ解説ツール【ピタゴラスの定理による斜辺の計算】
直角三角形の各辺:
・底辺(\( e_1 \) の大きさ):1
・高さ(\( e_2 \) の大きさ):\( \sqrt{3} \)
・斜辺(\( v \) の大きさ):\( |v| \)
ピタゴラスの定理を適用すると:
→ 横スクロールして下さい →
\[ \begin{aligned} |v|^2 &= 1^2 + (\sqrt{3})^2 \\[10pt] |v|^2 &= 1 + 3 \\[10pt] |v|^2 &= 4 \\[10pt] |v| &= 2 \end{aligned} \]【角度の計算】
合成ベクトルの角度 \( \phi \) は:
→ 横スクロールして下さい →
\[ \tan \phi = \frac{\sqrt{3}}{1} = \sqrt{3} \]よって \( \phi = \arctan(\sqrt{3}) = \frac{\pi}{3} \, \mathrm{[rad]} \) (60°)
完璧や!\( |v| = 2 \) で、角度が \( \frac{\pi}{3} \) やな。でもここで大事なことがあるで。
\( \tan \phi = \sqrt{3} \) のとき \( \phi = \frac{\pi}{3} \) っていうのは、よく出る三角比やから絶対覚えとかなアカン。特別な角度の三角比っていうんや。確認してみよう!

【特別な角度の三角比】
電験三種でよく出る重要な三角比の値:
30°(\( \frac{\pi}{6} \) rad)の場合:
\( \sin 30° = \frac{1}{2} \)、\( \cos 30° = \frac{\sqrt{3}}{2} \)、\( \tan 30° = \frac{1}{\sqrt{3}} \)
45°(\( \frac{\pi}{4} \) rad)の場合:
\( \sin 45° = \frac{1}{\sqrt{2}} \)、\( \cos 45° = \frac{1}{\sqrt{2}} \)、\( \tan 45° = 1 \)
60°(\( \frac{\pi}{3} \) rad)の場合:
\( \sin 60° = \frac{\sqrt{3}}{2} \)、\( \cos 60° = \frac{1}{2} \)、\( \tan 60° = \sqrt{3} \)
【今回の問題での確認】
\( \tan \phi = \sqrt{3} \) なので、\( \phi = 60° = \frac{\pi}{3} \, \mathrm{[rad]} \)
この関係は電験三種では頻出なので、必ず暗記しておきましょう。
図を見ると、底辺1、高さ\( \sqrt{3} \)の直角三角形で、斜辺が2、角度が60°となっていることが確認できます。
よっしゃ!三角比もばっちりやな。そしたら答えを整理してみよう。
(ア)合成電圧の最大値は \( e_1 \) の最大値の何倍か?
(イ)位相は \( e_1 \) を基準として何ラジアンか?
(ウ)その位相は進みか遅れか?
ベクトル図から読み取った結果をまとめてみよか。
【解答の整理】
(ア)最大値の倍率
計算結果:\( |v| = 2 \)
\( e_1 \) の最大値を1とした場合、合成電圧 \( v \) の最大値は2
したがって、合成電圧の最大値は \( e_1 \) の最大値の 2倍
(イ)位相差
計算結果:\( \phi = \frac{\pi}{3} \, \mathrm{[rad]} \)
合成電圧 \( v \) の位相は \( e_1 \) を基準として \( \frac{\pi}{3} \) ラジアン
(ウ)進みか遅れか
ベクトル図を見ると、合成ベクトル \( \vec{v} \) は基準ベクトル \( \vec{e_1} \) よりも反時計回りに回転した位置にあります。
反時計回りは進み位相を意味するので、進み
【選択肢との照合】
(ア)2、(イ)\( \frac{\pi}{3} \)、(ウ)進み → 選択肢(3)
完璧やな!答えは (3) で確定や。でも念のため、他の選択肢がなんでダメなのかも確認してみよう。
間違いやすいポイントを理解しておけば、同じような問題が出ても間違えんからな。どの選択肢がどんな間違いかを考えてみよか。
【他の選択肢の検討】
選択肢(1):\( \frac{1}{2} \)、\( \frac{\pi}{3} \)、進み
最大値が \( \frac{1}{2} \) は明らかに間違い。2つのベクトルを合成すれば、個々のベクトルより大きくなるはずです。
選択肢(2):\( 1+\sqrt{3} \)、\( \frac{\pi}{6} \)、遅れ
最大値 \( 1+\sqrt{3} \approx 2.73 \) は、ベクトルを算術的に足した値。これはベクトル合成ではなく、スカラー加算の間違い。また位相も角度も間違い。
選択肢(3):2、\( \frac{\pi}{3} \)、進み
✅ 正解!すべて計算結果と一致
選択肢(4):\( \sqrt{3} \)、\( \frac{\pi}{6} \)、遅れ
最大値が \( \sqrt{3} \) は \( e_2 \) の大きさと同じ。これは合成を間違えた結果。位相と進み遅れも間違い。
選択肢(5):2、\( \frac{2\pi}{3} \)、進み
最大値は正しいが、位相が \( \frac{2\pi}{3} \) は120°で間違い。
よし、選択肢の分析もばっちりやな!そしたら、この問題で重要な「進み遅れの判定」について、もうちょっと詳しく説明しとくで。
これ、電験三種では絶対に覚えとかなアカン基本やからな。ベクトル図でどうやって判定するか、しっかり理解しておこう。
【進み遅れの判定方法】
1. ベクトル図での判定
・基準ベクトル(今回は \( \vec{e_1} \))から見て:
- 反時計回り → 進み位相
- 時計回り → 遅れ位相
2. 数式での判定
位相差を \( \Delta \phi \) とすると:
・\( \Delta \phi > 0 \) → 進み位相
・\( \Delta \phi < 0 \) → 遅れ位相
3. 今回の問題での適用
\( e_1 \) の位相:0(基準)
\( v \) の位相:\( +\frac{\pi}{3} \)
位相差:\( \frac{\pi}{3} - 0 = +\frac{\pi}{3} > 0 \) → 進み
【記憶のポイント】
・時計の針と同じ向き(時計回り)= 時間が遅れる = 遅れ位相
・時計の針と逆向き(反時計回り)= 時間が進む = 進み位相
このイメージで覚えると間違えにくいです。
ナイス!進み遅れの判定もばっちりやな。そしたら最後に、この問題の解法パターンを整理しとこう。
交流の合成問題は電験三種でよく出るから、解法の手順をしっかり覚えといてや。どんな手順で解いたか振り返ってみよか?
【交流合成問題の標準解法手順】
ステップ1:問題の理解
・各交流電圧の最大値と位相を把握
・直列か並列かの接続方法を確認
・求めるものを明確化(最大値、位相、進み遅れ)
ステップ2:ベクトル図の作成
・基準となる電圧を水平右向きに設定
・他の電圧を適切な位相差で配置
・ベクトルの長さは最大値に比例させる
ステップ3:ベクトル合成
・直列接続 → ベクトルの加算
・並列接続 → 電流ベクトルの処理が必要
・幾何学的方法(三角比)または複素数計算
ステップ4:数値計算
・ピタゴラスの定理で合成ベクトルの大きさ
・逆三角関数で合成ベクトルの角度
・特別な角度(30°, 45°, 60°)の活用
ステップ5:結果の解釈
・最大値の倍率計算
・位相差の算出
・進み遅れの判定
よっしゃ!解法パターンも完璧やな。そしたら最後に、この問題で使った重要な知識をまとめとこう。
これらは電験三種の交流分野で何回も出てくる基本中の基本やから、絶対に覚えとかなアカンで!
【重要知識のまとめ】
1. 特別な角度の三角比(必須暗記)
・\( \tan 30° = \frac{1}{\sqrt{3}} \)、\( \tan 45° = 1 \)、\( \tan 60° = \sqrt{3} \)
・\( \sin 30° = \frac{1}{2} \)、\( \sin 60° = \frac{\sqrt{3}}{2} \)
・\( \cos 30° = \frac{\sqrt{3}}{2} \)、\( \cos 60° = \frac{1}{2} \)
2. ベクトル合成の基本
・直列接続では電圧ベクトルを加算
・ピタゴラスの定理:\( c^2 = a^2 + b^2 \)(直角の場合)
・一般的な合成:\( c^2 = a^2 + b^2 + 2ab\cos\theta \)
3. 位相の表現
・ラジアン表記:\( \pi \, \mathrm{rad} = 180° \)
・\( \frac{\pi}{6} = 30° \)、\( \frac{\pi}{4} = 45° \)、\( \frac{\pi}{3} = 60° \)
・進み遅れ:反時計回り = 進み、時計回り = 遅れ
4. 実用的なテクニック
・ベクトル図は必ず描く(視覚的理解が重要)
・基準を明確にして相対的に考える
・計算前に大まかな答えを予想する
・検算で答えの妥当性を確認する
【電験三種での応用範囲】
・RLC回路のインピーダンス合成
・三相交流の線間電圧と相電圧
・変圧器の等価回路
・電力の有効・無効・皮相成分
今日学んだベクトル合成の考え方は、これらすべての基礎になっています!
完璧や!ここまで理解できたら、交流の基本はバッチリやな。
最後に、この問題を通して学んだことを実際の電気回路でどう活かせるかも考えてみよう。交流回路は身の回りのあらゆる電気機器で使われてるからな。どんな場面で今日の知識が役立つと思う?
今日学んだ内容が実際にどこで使われているか、考えてみますと...
家庭のコンセントは100Vの交流ですが、これも正弦波ですよね。エアコンや冷蔵庫などの電化製品では、内部で複数の交流電圧が合成される場面があるのではないでしょうか。
また、工場などの三相交流では、3つの位相が120°ずつずれた交流が使われていると聞いたことがあります。今日のベクトル合成の考え方は、そういった複雑な交流システムを理解するための基礎になりそうです。
変圧器でも、一次側と二次側で電圧や位相の関係があるでしょうし、今日学んだ位相の進み遅れの概念が重要になるのかもしれません。
まだまだ実際の応用は難しく感じますが、今日の基本がとても大切だということは分かりました!
おお、すごいやん!よう考えられてるな〜。その通りや、今日学んだことは電気の世界のあちこちで使われてるんやで。
特に君が言った三相交流は、まさに今日のベクトル合成の応用や。3つの電圧が120°ずつずれてて、それらの合成で線間電圧ができるんや。工場の大型モーターなんかで使われてるで。
それから変圧器の位相関係、インバーターでの電圧制御、電力系統での力率改善なんかでも、今日の知識がめちゃくちゃ重要になってくるんや。
身近なところでは、LEDの調光回路とか、電子レンジのマグネトロンとか、パソコンの電源回路とかでも使われてるで。交流は本当に奥が深いんやで〜
先生のお話を聞いて、交流がこんなに身近で重要だとは思いませんでした!
三相交流での120°位相差は、今日の90°の場合の発展版なのですね。3つのベクトルを合成する計算は、今日の2つのベクトル合成より複雑になりそうですが、基本的な考え方は同じということでしょうか。
LEDの調光回路や電子レンジにも使われているというのは驚きです。普段何気なく使っている家電の中で、今日学んだベクトル合成が実際に働いているんですね。
力率改善という言葉は聞いたことがありますが、これも位相に関係があるのでしょうか。有効電力と無効電力の関係も、今日のベクトル図のような考え方で理解できるのかもしれませんね。
交流の世界がこんなに広くて深いとは...今日は本当に基礎中の基礎を学んだのだと実感しました。もっと勉強したくなってきました!
ええやん!その調子や。君の理解力と学習意欲、素晴らしいで〜
そうそう、力率改善もまさにベクトル図の世界や。有効電力、無効電力、皮相電力の関係は、今日やった直角三角形とそっくりなんやで。
そしたら最後に、今日の学習を振り返って、次にどんなことを勉強していけばええかアドバイスしとくわ。段階的にレベルアップしていけば、必ず電験三種に合格できるからな!
【今日の学習成果と次のステップ】
習得できたこと:
・交流電圧のベクトル表現方法
・ベクトル合成による電圧の加算
・ピタゴラスの定理と逆三角関数の活用
・進み遅れ位相の判定方法
・特別な角度の三角比の重要性
次に学ぶべき内容:
1. 複素数による交流計算
・ベクトル図を数式で表現する方法
・オイラーの公式の活用
2. RLC回路のインピーダンス
・抵抗、リアクタンスの合成
・共振現象の理解
3. 三相交流システム
・星形結線と三角形結線
・線間電圧と相電圧の関係
4. 電力の概念
・有効電力、無効電力、皮相電力
・力率と位相角の関係
今日の基礎がしっかりしているので、これらの発展内容も着実に理解できるはずです!
解説まとめ
問題回路図

■ 交流電圧の合成とベクトル表示とは
交流電圧の合成は、異なる位相を持つ正弦波電圧を直列接続した際の合成波形を求める計算です。交流回路では電圧や電流が時間とともに変化するため、ベクトル図(フェーザ図)を用いて視覚的に解析することが重要です。これは三相交流回路の解析や電力系統の運用において必須の技術となります。
■ 計算手順と公式
- 交流電圧の瞬時値表現
正弦波交流電圧の瞬時値は以下のように表されます。
\( v = V_m \sin(\omega t + \theta) \ \mathrm{[V]} \)
ここで、\( V_m \)は最大値(波高値)、\( \omega \)は角周波数、\( \theta \)は初期位相です。
- ベクトル表示(フェーザ表示)
交流電圧をベクトルで表現する際は、最大値を大きさとし、位相を角度とする極座標で表します。
\( \dot{V} = V_m \angle \theta \ \mathrm{[V]} \)
- ベクトル合成の法則
複数の交流電圧が直列接続された場合、ベクトルの和として合成電圧を求めます。
\( \dot{V}_{合成} = \dot{V}_1 + \dot{V}_2 + \cdots \)
- 三角比を用いた計算
ベクトル図から合成ベクトルの大きさと位相を三角関数で計算します。
■ 具体的な計算例
問題条件
- \( e_1 = E \sin(\omega t + \theta) \ \mathrm{[V]} \)
- \( e_2 = \sqrt{3}E \sin(\omega t + \theta + \frac{\pi}{2}) \ \mathrm{[V]} \)
- 直列接続により合成電圧 \( v = e_1 + e_2 \)
e₁基準のベクトル図

60度の三角比

ベクトル表示
\( e_1 \)を基準(実軸方向)とし、\( e_2 \)は90度進み位相とします。
\[ \begin{aligned} \dot{e}_1 &= E \angle 0° = E \\[5pt] \dot{e}_2 &= \sqrt{3}E \angle 90° = j\sqrt{3}E \end{aligned} \]合成電圧の計算
ベクトル和として合成電圧を求めます:
\[ \begin{aligned} \dot{v} &= \dot{e}_1 + \dot{e}_2 \\[5pt] &= E + j\sqrt{3}E \\[5pt] &= E(1 + j\sqrt{3}) \end{aligned} \](ア) 最大値の倍率計算
合成ベクトルの大きさを計算します:
\[ \begin{aligned} |\dot{v}| &= |E(1 + j\sqrt{3})| \\[5pt] &= E\sqrt{1^2 + (\sqrt{3})^2} \\[5pt] &= E\sqrt{1 + 3} \\[5pt] &= E\sqrt{4} = 2E \end{aligned} \]したがって、合成電圧の最大値は \( e_1 \) の最大値の 2倍です。
(イ) 位相の計算
合成ベクトルの位相角を計算します:
\[ \begin{aligned} \theta &= \tan^{-1}\left(\frac{\sqrt{3}E}{E}\right) \\[5pt] &= \tan^{-1}(\sqrt{3}) \\[5pt] &= \frac{\pi}{3} \ \mathrm{[rad]} = 60° \end{aligned} \](ウ) 位相の進み・遅れ
合成電圧の位相が正の値(\( +\frac{\pi}{3} \))なので、\( e_1 \) を基準として 進み位相です。
三角比による検証
直角三角形において:
- 底辺:\( E \)(\( e_1 \) の大きさ)
- 高さ:\( \sqrt{3}E \)(\( e_2 \) の大きさ)
- 斜辺:\( 2E \)(合成電圧の大きさ)
- 角度:\( 60° = \frac{\pi}{3} \ \mathrm{[rad]} \)
結論
| (ア) 最大値の倍率 | (イ) 位相 [rad] | (ウ) 進み・遅れ |
|---|---|---|
| 2 | \( \frac{\pi}{3} \) | 進み |
答え:(3)
■ 実務上の留意点
交流電圧の合成計算は、電力系統の運用や三相交流回路の解析において極めて重要な技術です。特に電力品質管理や保護継電器の設定において必須の知識となります。
- 三相交流システム:三相交流では120度ずつ位相の異なる3つの電圧が合成され、平衡時には中性点電圧が零となります
- 高調波解析:基本波と高調波の合成により実際の波形歪みを評価し、電力品質を管理します
- 電力系統の同期:発電機の並列運転時には、電圧の大きさと位相を正確に合わせる必要があります
- 保護継電器:故障時の電圧・電流ベクトルを解析して保護装置の動作を設定します
- 無効電力制御:電圧の位相関係から無効電力の流れを制御し、電圧安定性を維持します
- 計測精度:位相測定の誤差は電力測定や保護装置の誤動作につながるため、高精度な測定が必要です