【理論】令和6年 (下期) 問17|平板コンデンサ回路における合計電荷と絶縁破壊電圧の計算問題
図のように,十分大きい平らな金属板で覆われた床と平板電極とで作られる空気コンデンサが二つ並列接続されている。
二つの電極は床と平行であり,それらの面積は左側が \( A_1 = 10^{-3} \) [\( \mathrm{m}^2 \)],右側が \( A_2 = 10^{-2} \) [\( \mathrm{m}^2 \)] である。
床と各電極の間隔は,左側が \( d = 10^{-3} \) [m] で固定,右側が \( x \) [m] で可変,直流電源電圧は \( V_0 = 1000 \) [V] である。
次の (a) 及び (b) の問に答えよ。
ただし,空気の誘電率を \( \varepsilon = 8.85 \times 10^{-12} \) [F/m] とし,静電容量を考える際にコンデンサの端効果は無視できるものとする。
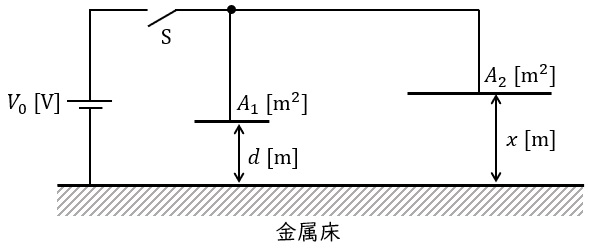
(a) まず,右側の \( x \) [m] を \( d \) [m] と設定し,スイッチ \( \mathrm{S} \) を一旦閉じてから開いた。
このとき,二枚の電極に蓄えられる合計電荷 \( Q \) の値 [C] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
(b) 上記 (a) の操作の後,徐々に \( x \) を増していったところ,\( x = 3.0 \times 10^{-3} \) [m] のときに左側の電極と床との間に火花放電が生じた。
左側のコンデンサの空隙(くうげき)の絶縁破壊電圧 \( V \) の値 [V] として,最も近いものを次の (1) ~ (5) のうちから一つ選べ。
合格への方程式
基本理論と公式

平行平板コンデンサの基本原理
平行平板コンデンサは、2枚の平行な金属板の間に絶縁体(この問題では空気)を挟んだ構造です。電荷を蓄える能力を静電容量といい、これは電池の容量とは全く違う概念です。
静電容量の基本公式
平行平板コンデンサの静電容量は以下の式で表されます:
\[ C = \frac{\varepsilon S}{d} \quad [\mathrm{F}] \]ここで、\( \varepsilon \):誘電率[F/m]、\( S \):極板面積[m²]、\( d \):極板間距離[m]
電荷・電圧・静電容量の関係
コンデンサに蓄えられる電荷量は、静電容量と電圧の積で決まります。これは水を入れるバケツの容量と水の高さの関係に似ています。
\[ Q = CV \quad [\mathrm{C}] \]コンデンサの接続方法
複数のコンデンサを接続する方法には並列接続と直列接続があります。
| 接続方法 | 合成静電容量 | 特徴 |
|---|---|---|
| 並列接続 | \( C = C_1 + C_2 + \cdots \) | 各コンデンサに同じ電圧がかかる |
| 直列接続 | \( \frac{1}{C} = \frac{1}{C_1} + \frac{1}{C_2} + \cdots \) | 各コンデンサに同じ電荷が蓄えられる |
覚え方のコツ
並列接続では「容量が足し算」、直列接続では「抵抗と同じように逆数の足し算」と覚えましょう。これは電流の流れ方の違いが関係しています。
誘電率について
誘電率は物質が電気を通しにくくする性質を表す値です。空気の誘電率は真空とほぼ同じで、\( 8.85 \times 10^{-12} \) F/mという非常に小さな値です。
身近な例で理解しよう
スマートフォンのタッチパネルも静電容量の変化を利用しています。指が画面に近づくと、指と画面の間に小さなコンデンサができて、その静電容量の変化を検出しているのです。
問題の理解と図解
回路構成の理解
この問題では、金属の床を共通の電極として、その上に2つの平行平板コンデンサが並列に接続されています。
回路の特徴
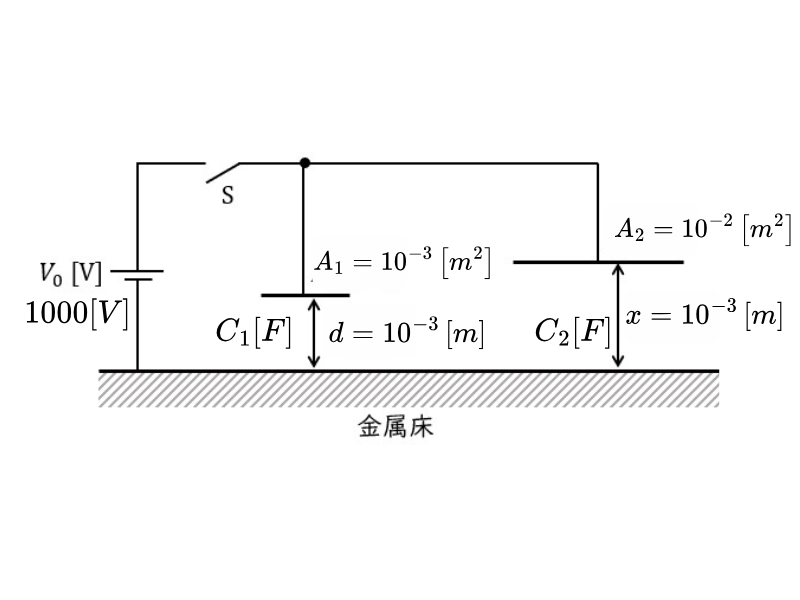
- 左側コンデンサ:面積 \( A_1 = 10^{-3} \) m²、間隔 \( d = 10^{-3} \) m(固定)
- 右側コンデンサ:面積 \( A_2 = 10^{-2} \) m²、間隔 \( x \) m(可変)
- 電源電圧:\( V_0 = 1000 \) V
- 空気の誘電率:\( \varepsilon = 8.85 \times 10^{-12} \) F/m
問題(a)の状況分析
最初に \( x = d = 10^{-3} \) mに設定し、スイッチを閉じてから開きます。この操作により:
- スイッチを閉じた瞬間:両方のコンデンサに1000Vが印加される
- コンデンサが充電される:それぞれの静電容量に応じて電荷が蓄積
- スイッチを開く:蓄積された電荷が保持される
並列接続の重要なポイント
並列接続では、各コンデンサに同じ電圧(この場合1000V)がかかります。しかし、蓄えられる電荷量は各コンデンサの静電容量によって決まります。
問題(b)の状況分析
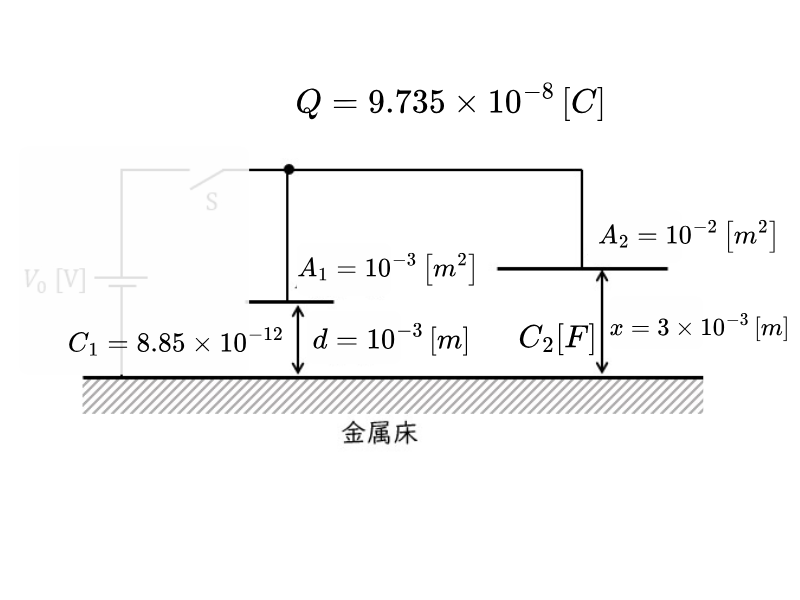
スイッチを開いた後、右側の間隔を \( x = 3.0 \times 10^{-3} \) mまで広げます。この時:
- 右側コンデンサの静電容量が減少
- 全体の合成静電容量も減少
- 電荷量は保持されるため、電圧が上昇
- 左側で絶縁破壊が発生
絶縁破壊とは
絶縁破壊は、電界の強さが限界を超えると絶縁体が電気を通すようになる現象です。空気中では雷も同じ現象です。一度破壊が起きると、急激に電流が流れて火花放電となります。
計算手順と解法
問題(a)の解法手順
ステップ1:各コンデンサの静電容量を計算
左側コンデンサ\( C_1 \)の静電容量:
\[ \begin{aligned} C_1 &= \frac{\varepsilon A_1}{d} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-3}}{10^{-3}} \\[10pt] &= 8.85 \times 10^{-12} \quad [\mathrm{F}] \end{aligned} \]右側コンデンサ\( C_2 \)の静電容量(\( x = d = 10^{-3} \)m のとき):
\[ \begin{aligned} C_2 &= \frac{\varepsilon A_2}{x} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{10^{-3}} \\[10pt] &= 8.85 \times 10^{-11} \quad [\mathrm{F}] \end{aligned} \]計算のポイント
右側のコンデンサは面積が10倍大きいので、同じ間隔なら静電容量も10倍になります。これは、面積が大きいほどたくさんの電荷を蓄えられるからです。
ステップ2:合成静電容量を計算
並列接続なので:
\[ C_{\mathrm{total}} = C_1 + C_2 = 8.85 \times 10^{-12} + 8.85 \times 10^{-11} = 9.735 \times 10^{-11} \quad [\mathrm{F}] \]ステップ3:合計電荷量を計算
\[ \begin{aligned} Q &= C_{\mathrm{total}} \times V_0 \\[10pt] &= 9.735 \times 10^{-11} \times 1000 \\[10pt] &= 9.735 \times 10^{-8} \approx 9.7 \times 10^{-8} \quad [\mathrm{C}] \end{aligned} \]答えの確認方法
計算結果が選択肢の中にあるかチェックしましょう。9.7×10⁻⁸ Cは選択肢(3)に該当します。
問題(b)の解法手順
ステップ1:変化後の右側静電容量を計算
\( x = 3.0 \times 10^{-3} \)m のときの\( C_2' \):
\[ \begin{aligned} C_2' &= \frac{\varepsilon A_2}{x} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{3.0 \times 10^{-3}} \\[10pt] &= 2.95 \times 10^{-11} \quad [\mathrm{F}] \end{aligned} \]ステップ2:新しい合成静電容量を計算
\[ C_{\mathrm{new}} = C_1 + C_2' = 8.85 \times 10^{-12} + 2.95 \times 10^{-11} = 3.835 \times 10^{-11} \quad [\mathrm{F}] \]ステップ3:絶縁破壊時の電圧を計算
電荷量は保持されるので:
\[ \begin{aligned} V &= \frac{Q}{C_{\mathrm{new}}} \\[10pt] &= \frac{9.735 \times 10^{-8}}{3.835 \times 10^{-11}} \\[10pt] &\approx 2.54 \times 10^3 \approx 2.5 \times 10^3 \quad [\mathrm{V}] \end{aligned} \]なぜ電圧が上がるのか
スイッチを開いた状態では電荷量が保持されます。右側の間隔を広げると合成静電容量が小さくなるため、V = Q/C の関係により電圧が上昇します。これは風船を膨らませると内部の圧力が高くなるのと似ています。
絶縁破壊現象と応用
絶縁破壊のメカニズム
絶縁破壊は、電界の強さが物質の絶縁限界を超えると発生する現象です。空気の場合、約3kV/mmが限界値とされています。
絶縁破壊の条件
電界の強さ \( E \) は以下の式で表されます:
\[ E = \frac{V}{d} \quad [\mathrm{V/m}] \]空気の絶縁破壊電界強度:約 \( 3 \times 10^6 \) V/m
この問題での絶縁破壊
左側のコンデンサで絶縁破壊が発生したのは、以下の理由からです:
- 左側の間隔(\( d = 10^{-3} \)m)が右側(\( x = 3.0 \times 10^{-3} \)m)より小さい
- 同じ電圧でも、間隔が小さいほど電界強度が大きくなる
- 左側の電界強度が先に限界値に達した
絶縁破壊の計算例
破壊時の電界強度を確認してみましょう:
\[ E_1 = \frac{V}{d} = \frac{2540}{10^{-3}} = 2.54 \times 10^6 \quad [\mathrm{V/m}] \]この値は空気の絶縁破壊電界強度に近く、計算の妥当性を示しています。
身近な絶縁破壊現象
- 雷:雲と地上の間の巨大な絶縁破壊
- 静電気の放電:乾燥した日にドアノブを触った時の小さな火花
- スパークプラグ:エンジンで燃料に点火するために意図的に絶縁破壊を起こす
実用上の注意点
高電圧機器の取り扱い
この問題のように、コンデンサの構造を変えると予想以上に高電圧が発生することがあります。実際の電気設備では:
- 適切な絶縁距離を確保する
- 絶縁材料の選定に注意する
- 湿度や温度による特性変化を考慮する
コンデンサの応用分野
| 応用分野 | 役割 | 特徴 |
|---|---|---|
| 電子回路 | ノイズ除去、信号結合 | 小容量、高速応答 |
| 電源回路 | 平滑化、電力貯蔵 | 大容量、高耐圧 |
| モーター始動 | 始動時の補助電源 | 瞬間的な大電流供給 |
| エネルギー貯蔵 | 瞬時電力補償 | 急速充放電可能 |
最新の技術動向
近年、電気自動車や再生可能エネルギーの普及により、大容量コンデンサ(スーパーキャパシタ)の需要が増加しています。これらは従来のコンデンサより大きな静電容量を持ち、瞬間的な大電力の供給や回収に使用されています。
問題解決のコツ
コンデンサ問題を解く時の手順
- 回路構成を正確に把握する(並列か直列か)
- 各コンデンサの静電容量を計算する
- 合成静電容量を求める
- 電荷保存則や電圧の関係を利用する
- 物理的な意味を考えて答えの妥当性を確認する
🔍 ワンポイントアドバイス: コンデンサ問題では「電荷保存」と「電圧の関係」が重要なポイントです。スイッチの開閉によって何が保持され、何が変化するかを必ず確認しましょう。また、並列接続では電圧が同じ、直列接続では電荷が同じという基本原則を忘れずに!
今日は並列接続されたコンデンサの問題やな!これは電験三種でもよく出る重要な分野やで。まず問題の回路図を見てもらおか。

床と平行な2つの平板電極があって、並列に接続されてるな。コンデンサの基本的な性質、覚えてるか?
はい、コンデンサは電荷を蓄える素子ですね。平行平板コンデンサの静電容量は次の式で表されます:
\[ C = \frac{\varepsilon S}{d} \]ここで、\( \varepsilon \) は誘電率、\( S \) は極板面積、\( d \) は極板間距離です。
そして電荷と静電容量、電圧の関係は \( Q = CV \) で表されます。
そうや!よく覚えてるな。今回は左側と右側に2つのコンデンサがあるねん。まず左側のコンデンサ \( C_1 \) の静電容量を計算してみよか。面積 \( A_1 = 10^{-3} \, \mathrm{m^2} \)、距離 \( d = 10^{-3} \, \mathrm{m} \) やで。
左側のコンデンサ \( C_1 \) の静電容量を計算します:
\[ \begin{aligned} C_1 &= \frac{\varepsilon A_1}{d} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-3}}{10^{-3}} \\[10pt] &= 8.85 \times 10^{-12} \, \mathrm{F} \end{aligned} \]正解や!次に右側のコンデンサ \( C_2 \) の静電容量を計算してみよか。(a)問題では \( x = d = 10^{-3} \, \mathrm{m} \) に設定するねん。面積は \( A_2 = 10^{-2} \, \mathrm{m^2} \) やで。
右側のコンデンサ \( C_2 \) の静電容量を計算します:
\[ \begin{aligned} C_2 &= \frac{\varepsilon A_2}{x} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{10^{-3}} \\[10pt] &= \frac{8.85 \times 10^{-14}}{10^{-3}} \\[10pt] &= 8.85 \times 10^{-11} \, \mathrm{F} \end{aligned} \]ええ感じや!ここで気づいた?右側のコンデンサの方が静電容量が大きいんやで。これは面積が10倍大きいからやな。並列接続の場合、合成静電容量はどうなるか覚えてるか?
はい、並列接続の場合、合成静電容量は各静電容量の和になります:
\[ \begin{aligned} C_{合計} &= C_1 + C_2 \\[10pt] &= 8.85 \times 10^{-12} + 8.85 \times 10^{-11} \\[10pt] &= 8.85 \times 10^{-12} + 88.5 \times 10^{-12} \\[10pt] &= 97.35 \times 10^{-12} \, \mathrm{F} \\[10pt] &= 9.735 \times 10^{-11} \, \mathrm{F} \end{aligned} \]そうや!ほんなら合計電荷 \( Q \) を求めてみよか。電圧は \( V_0 = 1000 \, \mathrm{V} \) やったな。\( Q = CV \) の関係を使うで。
合計電荷を計算します:
\[ \begin{aligned} Q &= C_{合計} \times V_0 \\[10pt] &= 9.735 \times 10^{-11} \times 1000 \\[10pt] &= 9.735 \times 10^{-8} \, \mathrm{C} \end{aligned} \]これは約 \( 9.7 \times 10^{-8} \, \mathrm{C} \) になります。
完璧や!(a)の答えは (3) の \( 9.7 \times 10^{-8} \, \mathrm{C} \) やな。ここで実際の状況を図で確認してみよか。

この状態でスイッチSを開いたら、電荷が保存されるんやで。ここが重要なポイントや!
はい、スイッチを開くと電源から切り離されるため、コンデンサに蓄えられた電荷 \( Q = 9.735 \times 10^{-8} \, \mathrm{C} \) が保存されます。
これは電荷保存の法則に基づいており、この後の(b)問題で重要な条件となります。
つまり、\( x \) を変化させても合計電荷量は変わらないということですね。
その通りや!よう理解してるな。ほんなら(b)問題に進もか。\( x = 3.0 \times 10^{-3} \, \mathrm{m} \) に変えた時の図を見てみよか。

\( x \) が3倍になったから、右側のコンデンサ \( C_2 \) の静電容量はどうなると思う?
静電容量は極板間距離に反比例するので、距離が3倍になると静電容量は1/3になります。
新しい \( C_2' \) を計算してみます:
\[ \begin{aligned} C_2' &= \frac{\varepsilon A_2}{x} \\[10pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{3.0 \times 10^{-3}} \\[10pt] &= \frac{8.85 \times 10^{-14}}{3.0 \times 10^{-3}} \\[10pt] &= 2.95 \times 10^{-11} \, \mathrm{F} \end{aligned} \]正解や!元の \( C_2 = 8.85 \times 10^{-11} \, \mathrm{F} \) の約1/3になったな。ほんなら新しい合成静電容量を計算してみよか。
新しい合成静電容量を計算します:
\[ \begin{aligned} C_{新} &= C_1 + C_2' \\[10pt] &= 8.85 \times 10^{-12} + 2.95 \times 10^{-11} \\[10pt] &= 8.85 \times 10^{-12} + 29.5 \times 10^{-12} \\[10pt] &= 38.35 \times 10^{-12} \, \mathrm{F} \\[10pt] &= 3.835 \times 10^{-11} \, \mathrm{F} \end{aligned} \]ええ計算や!静電容量が小さくなったのに電荷は保存されてるから、電圧はどうなると思う?\( Q = CV \) から \( V = \frac{Q}{C} \) やろ?
はい、電荷が保存されているので、電圧は上昇します。計算してみます:
\[ \begin{aligned} V &= \frac{Q}{C_{新}} \\[10pt] &= \frac{9.735 \times 10^{-8}}{3.835 \times 10^{-11}} \\[10pt] &= 2.54 \times 10^3 \, \mathrm{V} \end{aligned} \]約2540Vになりました。元の1000Vから大幅に上昇していますね。
完璧や!電圧が2.5倍以上に上がったな。この高電圧で左側のコンデンサに火花放電が起こったんやで。ということは、この2540Vが左側コンデンサの絶縁破壊電圧っちゅうことや。選択肢を見ると、どれが一番近い?
計算結果は約 \( 2.54 \times 10^3 = 2540 \, \mathrm{V} \) でした。
選択肢を確認すると:
(1) \( 3.3 \times 10^2 = 330 \, \mathrm{V} \)
(2) \( 2.5 \times 10^3 = 2500 \, \mathrm{V} \)
(3) \( 3.0 \times 10^3 = 3000 \, \mathrm{V} \)
(4) \( 5.1 \times 10^3 = 5100 \, \mathrm{V} \)
(5) \( 3.0 \times 10^4 = 30000 \, \mathrm{V} \)
2540Vに最も近いのは (2) \( 2.5 \times 10^3 \, \mathrm{V} \) ですね。
正解や!(b)の答えは (2) の \( 2.5 \times 10^3 \, \mathrm{V} \) やな。ところで、なんで左側のコンデンサだけに火花放電が起こったと思う?
並列接続されているコンデンサには同じ電圧がかかります。しかし、電界の強さは電圧を距離で割った値になります。
左側:電界 = \( \frac{V}{d} = \frac{2540}{10^{-3}} = 2.54 \times 10^6 \, \mathrm{V/m} \)
右側:電界 = \( \frac{V}{x} = \frac{2540}{3.0 \times 10^{-3}} = 8.47 \times 10^5 \, \mathrm{V/m} \)
左側の方が電界強度が高いため、絶縁破壊が先に起こったということですね。
すばらしい分析や!電界強度の概念もよう理解してるな。実は空気の絶縁破壊電界は約 \( 3 \times 10^6 \, \mathrm{V/m} \) やから、左側がちょうど限界に達したっちゅうことやな。最後に今回の問題のポイントをまとめてみよか。
今回の重要ポイントをまとめます:
1. 平行平板コンデンサの静電容量
\( C = \frac{\varepsilon S}{d} \) で、面積に比例、距離に反比例
2. 並列接続の特性
合成静電容量:\( C = C_1 + C_2 \)、各コンデンサに同じ電圧
3. 電荷保存則
スイッチを開いた後は電荷が保存される:\( Q = \text{一定} \)
4. 静電容量変化の影響
\( Q = CV \) より、\( C \) が小さくなると \( V \) が大きくなる
5. 絶縁破壊の条件
電界強度 \( E = \frac{V}{d} \) が限界値を超えると放電発生
6. 実用的知識
空気の絶縁破壊電界:約 \( 3 \times 10^6 \, \mathrm{V/m} \)
完璧やな!この問題は高電圧技術の基礎でもあるんやで。実際の高圧機器でも絶縁設計は非常に重要や。コンデンサの静電容量が変わると電圧が変化するっちゅう現象は、可変コンデンサや静電気の蓄積でもよく見られるから、しっかり理解しといてな!
ありがとうございました!コンデンサの基本特性と高電圧現象がよく理解できました。
実用面での豆知識:
この原理は雷の発生メカニズムにも関係しています。雲と地面の間の距離が変わると電界強度が変化し、限界を超えると放電(雷)が起こります。また、電子機器の静電気対策でも同様の現象が考慮されています。
覚え方のコツ:
「静電容量が小さくなると電圧が大きくなる」→「器が小さくなると水位が上がる」と覚えると理解しやすいです。
計算のポイント:
指数計算では桁数を間違えやすいので、各ステップで単位と桁数を確認することが重要です。
解説まとめ
問題回路図

■ 並列コンデンサと絶縁破壊とは
並列接続されたコンデンサは、電力系統や電子機器において重要な役割を果たします。平行平板コンデンサでは、極板間距離の変化により静電容量が変化し、蓄積電荷が再分配されます。絶縁破壊は、コンデンサの極板間に過大な電界が発生し、絶縁物質が電気的に破壊される現象で、電力機器の設計や保護において重要な考慮事項となります。
■ 計算手順と公式
平行平板コンデンサの静電容量
極板面積と極板間距離により静電容量が決まります。
静電容量:\( C = \frac{\varepsilon S}{d} \ \mathrm{[F]} \)
ε:誘電率 [F/m]、S:極板面積 [m²]、d:極板間距離 [m]
電荷と電圧の関係
コンデンサの基本的な関係式です。
電荷:\( Q = CV \ \mathrm{[C]} \)
電圧:\( V = \frac{Q}{C} \ \mathrm{[V]} \)
並列コンデンサの合成静電容量
並列接続では静電容量が加算されます。
並列合成:\( C_{合成} = C_1 + C_2 + \cdots \)
電荷保存の法則
スイッチを開いた後は総電荷量が保存されます。
電荷保存:\( Q_{total} = \text{一定} \)
■ 具体的な計算例
問題条件
左側コンデンサ:A₁=10⁻³m²、d=10⁻³m(固定)、右側コンデンサ:A₂=10⁻²m²、x=可変、電源電圧:V₀=1000V、空気の誘電率:ε=8.85×10⁻¹²F/m
(a) 合計電荷の計算
x = d に設定した状態

Step 1: 左側コンデンサの静電容量
\[ \begin{aligned} C_1 &= \frac{\varepsilon A_1}{d} \\[5pt] &= \frac{8.85 \times 10^{-12} \times 10^{-3}}{10^{-3}} \\[5pt] &= 8.85 \times 10^{-12} \ \mathrm{[F]} \end{aligned} \]Step 2: 右側コンデンサの静電容量(x = d = 10⁻³m)
\[ \begin{aligned} C_2 &= \frac{\varepsilon A_2}{x} \\[5pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{10^{-3}} \\[5pt] &= \frac{8.85 \times 10^{-14}}{10^{-3}} \\[5pt] &= 8.85 \times 10^{-11} \ \mathrm{[F]} \end{aligned} \]Step 3: 並列合成静電容量
\[ \begin{aligned} C_{合成} &= C_1 + C_2 \\[5pt] &= 8.85 \times 10^{-12} + 8.85 \times 10^{-11} \\[5pt] &= 8.85 \times 10^{-12} + 88.5 \times 10^{-12} \\[5pt] &= 97.35 \times 10^{-12} \ \mathrm{[F]} \end{aligned} \]Step 4: 合計電荷の計算
\[ \begin{aligned} Q &= C_{合成} \times V_0 \\[5pt] &= 97.35 \times 10^{-12} \times 1000 \\[5pt] &= 97.35 \times 10^{-9} \\[5pt] &= 9.735 \times 10^{-8} \\[5pt] &\approx 9.7 \times 10^{-8} \ \mathrm{[C]} \end{aligned} \](b) 絶縁破壊電圧の計算
x = 3.0×10⁻³m に変更した状態

Step 1: x変更後の右側コンデンサ静電容量
\[ \begin{aligned} C_2' &= \frac{\varepsilon A_2}{x} \\[5pt] &= \frac{8.85 \times 10^{-12} \times 10^{-2}}{3.0 \times 10^{-3}} \\[5pt] &= \frac{8.85 \times 10^{-14}}{3.0 \times 10^{-3}} \\[5pt] &= 2.95 \times 10^{-11} \ \mathrm{[F]} \end{aligned} \]Step 2: 新しい合成静電容量
\[ \begin{aligned} C_{新} &= C_1 + C_2' \\[5pt] &= 8.85 \times 10^{-12} + 2.95 \times 10^{-11} \\[5pt] &= 8.85 \times 10^{-12} + 29.5 \times 10^{-12} \\[5pt] &= 38.35 \times 10^{-12} \ \mathrm{[F]} \end{aligned} \]Step 3: 電荷保存による電圧計算
スイッチを開いた後は総電荷量が保存されるため:
\[ \begin{aligned} V &= \frac{Q}{C_{新}} \\[5pt] &= \frac{9.735 \times 10^{-8}}{38.35 \times 10^{-12}} \\[5pt] &= \frac{9.735 \times 10^{-8}}{3.835 \times 10^{-11}} \\[5pt] &= 2.54 \times 10^3 \\[5pt] &\approx 2.5 \times 10^3 \ \mathrm{[V]} \end{aligned} \]Step 4: 絶縁破壊電圧の意味
左側のコンデンサで火花放電が発生したということは、この電圧2500Vが左側コンデンサの絶縁破壊電圧に相当します。
電荷保存と静電容量変化の関係
スイッチを開いた後、右側コンデンサの極板間距離を増加させると静電容量が減少します。総電荷量は保存されるため、合成静電容量の減少により端子電圧が上昇し、ついには絶縁破壊に至ります。
計算結果まとめ
| 項目 | 記号 | 値 | 単位 |
|---|---|---|---|
| 左側静電容量 | \( C_1 \) | 8.85×10⁻¹² | F |
| 右側静電容量(初期) | \( C_2 \) | 8.85×10⁻¹¹ | F |
| 初期合成静電容量 | \( C_{合成} \) | 9.735×10⁻¹¹ | F |
| 合計電荷 | \( Q \) | 9.7×10⁻⁸ | C |
| 右側静電容量(変更後) | \( C_2' \) | 2.95×10⁻¹¹ | F |
| 絶縁破壊電圧 | \( V \) | 2.5×10³ | V |
結論:
(a) 合計電荷 Q = 9.7×10⁻⁸ C 答え:(3)
(b) 絶縁破壊電圧 V = 2.5×10³ V 答え:(2)
■ 実務上の留意点
コンデンサの絶縁破壊は、電力機器や電子機器において重大な事故につながる可能性があります。特に高電圧機器の設計・運用において重要な考慮事項となります。
絶縁協調設計:機器の絶縁レベルは想定される最大電圧の1.5~2倍程度の安全率を見込んで設計する必要があります。雷サージや開閉サージによる過電圧も考慮します。コンデンサバンクの保護:力率改善用コンデンサでは、過電圧保護継電器による保護が重要です。調波電圧の重畳による実効電圧の上昇も監視する必要があります。絶縁診断技術:部分放電測定や絶縁抵抗測定により絶縁劣化を早期に発見し、絶縁破壊を未然に防ぐ予防保全が重要です。
環境条件の影響:湿度、温度、汚損などの環境条件により絶縁破壊電圧は大きく変化するため、運用環境を考慮した設計が必要です。電界集中対策:電極の形状や配置により電界集中が発生し、局所的な絶縁破壊が起こる場合があります。適切な電極設計と絶縁距離の確保が重要です。老朽化対策:長期間使用されたコンデンサでは絶縁材料の劣化により絶縁破壊電圧が低下するため、定期的な絶縁診断と計画的な更新が必要です。安全対策:コンデンサの点検・交換作業では残留電荷による感電事故を防ぐため、適切な放電手順と保護具の使用が必要です。