【理論】令和1年 問9|RLC並列回路における角周波数変化と電流実効値の関係に関する計算問題
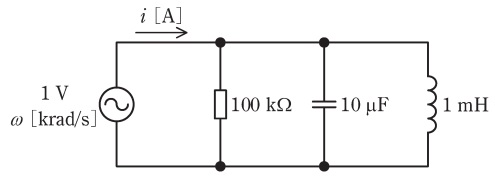
図は,実効値が \( 1 \) [V] で角周波数 \( \omega \) [krad/s] が変化する正弦波交流電源を含む回路である。
いま,\( \omega \) の値が \( \omega_1 = 5 \) [krad/s],\( \omega_2 = 10 \) [krad/s],\( \omega_3 = 30 \) [krad/s] の3通りの場合を考え,\( \omega = \omega_{\mathrm{k}} \ (k = 1, 2, 3) \) のときの電流 \( i \) [A] の実効値を \( I_{\mathrm{k}} \) と表す。
\( I_1 \),\( I_2 \),\( I_3 \) の大小関係として,正しいものを次の (1)~(5) のうちから一つ選べ。
(1) \( I_1 < I_2 < I_3 \)
(2) \( I_1 = I_2 < I_3 \)
(3) \( I_2 < I_1 < I_3 \)
(4) \( I_2 < I_1 = I_3 \)
(5) \( I_3 < I_2 < I_1 \)
合格への方程式
共振回路の基本原理
共振とは
共振とは、交流回路において電圧と電流が同位相になる状態のことです。この状態では、回路の性質に応じて「リアクタンスが0」または「サセプタンスが0」となります。身近な例えでは、ブランコを押すタイミングと同じで、エネルギーの伝達が最も効率よく行われる状態と考えられます。
共振回路は、コイル(L)とコンデンサ(C)という2つの異なるエネルギー貯蔵素子で構成されます。コイルは電流によって磁界のエネルギーを蓄え、コンデンサは電圧によって電界のエネルギーを蓄えます。
共振の種類
共振回路には大きく分けて2種類あります:
- 直列共振回路:LとCが直列に接続され、リアクタンスが0になる状態
- 並列共振回路:LとCが並列に接続され、サセプタンスが0(リアクタンスが無限大)になる状態
共振の応用
共振回路は、ラジオやテレビのチューナー、無線通信機器など、特定の周波数を選択する回路として広く利用されています。
直列共振回路
直列共振回路の定義
直列共振回路とは、抵抗R、インダクタンスL、キャパシタンスCが直列に接続された回路で、特定の周波数(共振周波数)において回路のリアクタンスが0になる状態を共振と呼びます。
直列共振回路では、コイルとコンデンサのリアクタンスが大きさは同じで符号が反対になるため、互いに打ち消し合います。これにより、回路のインピーダンスは純抵抗性(抵抗Rの値)となります。
直列回路の共振条件
共振条件は電圧と電流が同位相になる状態で、回路のリアクタンスが零になる状態のことを言います。
\[ \begin{aligned} \mathrm{j}\omega L + \frac{1}{\mathrm{j}\omega C} &= 0 \\[10pt] \mathrm{j}\left(\omega L - \frac{1}{\omega C}\right) &= 0 \\[10pt] \omega L &= \frac{1}{\omega C} \end{aligned} \]の時共振となり、その共振角周波数と共振周波数は、上式を \(\omega\) について整理すると、
\[ \begin{aligned} \omega^2 &= \frac{1}{LC} \\[10pt] \omega &= \frac{1}{\sqrt{LC}} \\[10pt] f &= \frac{1}{2\pi\sqrt{LC}} \end{aligned} \]で求められます。
直列共振回路の特性
- 共振状態では、回路のインピーダンスが最小(純抵抗R)になります
- 電流が最大になります
- コイルとコンデンサの端子電圧は、印加電圧よりも大きくなることがあります
並列共振回路
並列共振回路の定義
並列共振回路とは、抵抗R、インダクタンスL、キャパシタンスCが並列に接続された回路で、特定の周波数(共振周波数)において回路のサセプタンスが0(リアクタンスが無限大)になる状態を共振と呼びます。
並列共振回路では、コイル回路とコンデンサ回路を流れる電流は大きさが同じで向きが逆になるため、互いに打ち消し合います。これにより、回路のインピーダンスは最大となります。
並列回路の共振条件
共振条件は電圧と電流が同位相になる状態で、回路のサセプタンスが零(リアクタンスが無限大)になる状態のことを言います。
\[ \begin{aligned} \mathrm{j}\omega C + \frac{1}{\mathrm{j}\omega L} &= 0 \\[10pt] \mathrm{j}\left(\omega C - \frac{1}{\omega L}\right) &= 0 \\[10pt] \omega C &= \frac{1}{\omega L} \end{aligned} \]の時共振となり、その共振角周波数と共振周波数は、
\[ \begin{aligned} \omega &= \frac{1}{\sqrt{LC}} \\[10pt] f &= \frac{1}{2\pi\sqrt{LC}} \end{aligned} \]で求められます。
並列共振回路の特性
- 共振状態では、回路のインピーダンスが最大になります
- 電流が最小になります
- 内部循環電流(LとC間を流れる電流)は、電源電流よりも大きくなることがあります
計算例題
例題1: 直列共振回路の共振周波数
インダクタンス L = 4 mH、キャパシタンス C = 0.4 μF の直列回路の共振周波数を求めよ。
解答
直列共振回路の共振周波数の式は:
\[ f = \frac{1}{2\pi\sqrt{LC}} \]値を代入すると:
\[ \begin{aligned} f &= \frac{1}{2\pi\sqrt{4 \times 10^{-3} \times 4 \times 10^{-7}}} \\[10pt] &= \frac{1}{2\pi\sqrt{16 \times 10^{-10}}} \\[10pt] &= \frac{1}{2\pi \times 4 \times 10^{-5}} \\[10pt] &= \frac{10^5}{8\pi} \\[10pt] &\approx 3979 \mathrm{\ Hz} \approx 4 \mathrm{\ kHz} \end{aligned} \]よって、共振周波数は約 4 kHz です。
例題2: 並列共振回路のインダクタンス
共振周波数が 5 kHz で、キャパシタンス C = 1 μF の並列回路のインダクタンス L を求めよ。
解答
並列共振回路の共振周波数の式は:
\[ f = \frac{1}{2\pi\sqrt{LC}} \]この式を L について解くと:
\[ \begin{aligned} L &= \frac{1}{(2\pi f)^2 C} \\[10pt] &= \frac{1}{(2\pi \times 5 \times 10^3)^2 \times 10^{-6}} \\[10pt] &= \frac{1}{(10\pi \times 10^3)^2 \times 10^{-6}} \\[10pt] &= \frac{10^6}{(10\pi)^2 \times 10^6} \\[10pt] &= \frac{1}{(10\pi)^2} \\[10pt] &\approx 1.01 \times 10^{-3} \mathrm{\ H} = 1.01 \mathrm{\ mH} \end{aligned} \]よって、必要なインダクタンスは約 1.01 mH です。
計算時の注意点
共振周波数の計算では、単位を揃えることが重要です。特に:
- インダクタンス L は通常 H(ヘンリー)単位
- キャパシタンス C は通常 F(ファラド)単位
- 周波数 f は Hz(ヘルツ)単位
- 角周波数 ω は rad/s 単位
また、mH や μF などの単位を使う場合は、計算時に基本単位(H, F)に変換しましょう。
🔍 ワンポイントアドバイス: 直列共振と並列共振の共振周波数の公式は同じ形(f = 1/(2π√LC))ですが、回路特性は逆になります。直列共振ではインピーダンスが最小(電流最大)、並列共振ではインピーダンスが最大(電流最小)になることを覚えておきましょう。覚え方としては「直列=電流直進(最大)」、「並列=電流阻止(最小)」というイメージが役立ちます。
よっしゃ、今日は並列RLC回路の周波数に対する電流特性について勉強していくで!まずは回路図を見てみよか。交流電源に対して抵抗100k\(\Omega\)、コンデンサ10\(\mu\)F、インダクタ1mHが並列に接続されとるな。角周波数\(\omega\)が3つの値(5krad/s、10krad/s、30krad/s)の場合での電流の大きさを比較する問題や。まず、この回路のインピーダンスとか電流の求め方について考えてみようか?
はい、並列回路の場合はインピーダンスではなくアドミタンスで考えるのが便利だと思います。並列回路の全体のアドミタンスは各素子のアドミタンスの和になりますので、まず各素子のアドミタンスを求めて合成することになります。
抵抗のアドミタンスは1/R、コンデンサのアドミタンスはjωC、インダクタのアドミタンスは1/(jωL)となります。これらを合成して電流を求めていくことになりますね。
その通りや!並列回路やから、アドミタンスで考えるんが基本やな。じゃあ、この回路全体のアドミタンスȲを式で表してみてくれるか?抵抗が100kΩ、コンデンサが10μF、インダクタが1mHの場合や。
はい、全体のアドミタンスȲを求めます。
抵抗のアドミタンス = \( \frac{1}{R} = \frac{1}{100 \times 10^3} = 10^{-5} \ \mathrm{[S]} \)
コンデンサのアドミタンス = \( j\omega C = j\omega \times 10 \times 10^{-6} = j\omega \times 10^{-5} \ \mathrm{[S]} \)
インダクタのアドミタンス = \( \frac{1}{j\omega L} = \frac{1}{j\omega \times 1 \times 10^{-3}} = \frac{-j}{\omega \times 10^{-3}} \ \mathrm{[S]} \)
全体のアドミタンスȲは、これらの和になりますので:
→ 横スクロールして下さい →
\[ \begin{aligned} \dot{Y} &= \frac{1}{R} + j\omega C + \frac{1}{j\omega L} \\ &= \frac{1}{R} + j\omega C - \frac{j}{\omega L} \\[10pt] \dot{Y} &= 10^{-5} + j\omega \times 10^{-5} - \frac{j}{\omega \times 10^{-3}} \\ &= 10^{-5} + j\left( \omega \times 10^{-5} - \frac{1}{\omega \times 10^{-3}} \right) \end{aligned} \]
これが全体のアドミタンスの複素表現となります。
ええやん!アドミタンスの式がちゃんと出せたな。せやけど、電流の実効値を比較するためには、アドミタンスの「大きさ」が必要になるんやけど、どうやって求めるか分かるかな?複素アドミタンスȲから、大きさのYを求める方法を教えてくれるか?
はい、複素アドミタンスȲから大きさYを求めるには、複素数の絶対値を計算します。
複素アドミタンスȲは次のように表されました:
\( \dot{Y} = 10^{-5} + j\left(\omega \times 10^{-5} - \frac{1}{\omega \times 10^{-3}}\right) \)
複素数の絶対値は、実部と虚部の二乗和の平方根で求められますので:
→ 横スクロールして下さい →
\[ \begin{aligned} Y &= |\dot{Y}| = \sqrt{\left(10^{-5}\right)^2 + \left(\omega \times 10^{-5} - \frac{1}{\omega \times 10^{-3}}\right)^2} \\[10pt] &= \sqrt{\left(\frac{1}{R}\right)^2 + \left(\omega C - \frac{1}{\omega L}\right)^2} \end{aligned} \]これがアドミタンスの大きさを表す式となります。電流の実効値はこのアドミタンスの大きさと電圧の実効値の積になります。
ナイス!アドミタンスの大きさの式が出せたな。んで、電流の実効値I = V × Yになるから、電圧は1Vで共通やから、結局アドミタンスYの大きさが大きい方が電流も大きくなるわけや。
さて、この式を見てほしいんやけど、Yの大きさを決めるのは2つの要素があるよな。\( \left(\frac{1}{R}\right)^2 \)と\( \left(\omega C - \frac{1}{\omega L}\right)^2 \)や。この式から何か気づくことはあるかな?
はい、アドミタンスの大きさの式を見ると、2つの要素があることに気づきます。
1つ目は抵抗成分 \( \left(\frac{1}{R}\right)^2 \) で、これは角周波数ωに依存しない定数です。この問題では R = 100kΩ なので、\( \frac{1}{R} = 10^{-5} \) [S] となり、どの角周波数でも同じ値になります。
2つ目はリアクタンス成分 \( \left(\omega C - \frac{1}{\omega L}\right)^2 \) で、これは角周波数ωによって変化します。コンデンサのリアクタンスはωに比例して増加し、インダクタのリアクタンスはωに反比例して減少します。
特に重要な点として、\( \omega C - \frac{1}{\omega L} = 0 \) となる特定の角周波数が存在する場合、リアクタンス成分が0になり、アドミタンスは最小値 \( \frac{1}{R} \) となります。これが並列共振の条件で、このときに回路の電流は最小になります。
よう理解してるやん!そうや、\( \omega C - \frac{1}{\omega L} = 0 \)のときが並列共振状態になって、アドミタンスが最小(つまり電流も最小)になるんや。
じゃあ、この回路の共振角周波数 \( \omega_r \) を求めていこか。まずは条件式 \( \omega C - \frac{1}{\omega L} = 0 \) からスタートや。これを変形してみてくれるか?
はい、共振角周波数を求めるために、条件式 \( \omega C - \frac{1}{\omega L} = 0 \) を変形します。
まず、左辺の項を右辺に移項します:
\( \omega C = \frac{1}{\omega L} \)
この式から、ωについて解いていくことで共振角周波数が求められますね。
そうそう、ええ感じや!次はω²の式にしていきたいんやけど、どうやって変形したらええかな?
ω²の式にするために、両辺にωをかけてみます。
\( \omega C = \frac{1}{\omega L} \)
両辺にωをかけると:
\( \omega^2 C = \frac{1}{L} \)
これでω²を含む式に変形できました。
ナイス!これからω²について解いていくんやな。ω²がどうなるか、次のステップを教えてくれるか?
はい、ω²について解いていきます。
今、\( \omega^2 C = \frac{1}{L} \) という式が得られました。
両辺をCで割ると:
\( \omega^2 = \frac{1}{LC} \)
これでω²の値が求まりました。
ええやん!あともう一歩や。ω²からωの式、つまり共振角周波数 \( \omega_r \) の式にするにはどうしたらええかな?
ω²からωを求めるには、両辺の平方根をとります。
\( \omega^2 = \frac{1}{LC} \)
両辺の平方根をとると:
\( \omega = \pm\sqrt{\frac{1}{LC}} = \pm\frac{1}{\sqrt{LC}} \)
角周波数ωは正の値なので:
\( \omega_r = \frac{1}{\sqrt{LC}} \)
これが並列共振回路の共振角周波数の一般式となります。
素晴らしい!これで共振角周波数の一般式 \( \omega_r = \frac{1}{\sqrt{LC}} \) が導けたな。さあ、次はこの問題の具体的な値を代入して計算してみようか。L = 1mH = 10⁻³ H、C = 10μF = 10⁻⁵ F やな。
はい、求めた一般式に具体的な値を代入して計算します。
共振角周波数 \( \omega_r = \frac{1}{\sqrt{LC}} \) に、L = 1mH = 10⁻³ H、C = 10μF = 10⁻⁵ Fを代入します。
ただし、C = 10μF = 10×10⁻⁶ F = 10⁻⁵ Fではなく、C = 10μF = 10×10⁻⁶ Fですので、正確に計算します。
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{L \times C}} \\[10pt] &= \frac{1}{\sqrt{1 \times 10^{-3} \times 10 \times 10^{-6}}} \end{aligned} \]そうやな、C = 10μF = 10×10⁻⁶ F やね。計算を続けてくれるか?指数部分をまとめると計算しやすくなるで!
はい、指数部分をまとめて計算を続けます。
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{1 \times 10^{-3} \times 10 \times 10^{-6}}} \\[10pt] &= \frac{1}{\sqrt{10 \times 10^{-9}}} \end{aligned} \]指数部分を整理しました。10⁻³×10⁻⁶ = 10⁻⁹ ですね。次に平方根の計算を進めます。
ええ感じや!平方根の計算をしていこか。\( \sqrt{10 \times 10^{-9}} \) の計算は少し工夫が必要やな。どうやって計算するのが良いやろうか?
平方根の計算を工夫して進めます。まず、指数部分を変形します。
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{10 \times 10^{-9}}} \\[10pt] &= \frac{1}{\sqrt{10} \times \sqrt{10^{-9}}} \end{aligned} \]ここで、\( \sqrt{10^{-9}} = 10^{-\frac{9}{2}} = 10^{-4.5} \) となります。
したがって:
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{10} \times 10^{-4.5}} \\[10pt] &= \frac{10^{4.5}}{\sqrt{10}} \end{aligned} \]ええ計算の仕方やな!最後に数値として表してみよか。\( \frac{10^{4.5}}{\sqrt{10}} \) はどのくらいの値になるんやろか?
最後に数値として表します。
\( \sqrt{10} \) は約3.16なので:
\[ \begin{aligned} \omega_r &= \frac{10^{4.5}}{\sqrt{10}} \\[10pt] &= \frac{10^{4.5}}{3.16} \\[10pt] \end{aligned} \]ここで10の4.5乗を計算すると:
\[ \begin{aligned} 10^{4.5} &= 10^4 \times 10^{0.5} \\ &= 10,000 \times \sqrt{10} \\[10pt] &\approx 10,000 \times 3.16 \\ &\approx 31,600 \end{aligned} \]
\[ \begin{aligned} &\approx \frac{31600}{3.16} \\[10pt] &\approx 10000 \ \mathrm{[rad/s]} \\[10pt] &= 10 \ \mathrm{[krad/s]} \end{aligned} \]したがって、この回路の共振角周波数は約10,000 [rad/s] = 10 [krad/s]となります。
完璧やな!共振角周波数が \( \omega_r = 10 \) [krad/s] と求まったな。これは問題で与えられた \( \omega_2 = 10 \) [krad/s] と一致しとるな。つまり \( \omega_2 \) のときは共振状態になって、電流が最小になるわけや!
せやから \( I_2 \) が3つの中で一番小さいことがわかったわけやな。じゃあ次に、残りの \( I_1 \) と \( I_3 \) の大小関係を判断するにはどうしたらええやろか?
I₁とI₃の大小関係を判断するために、それぞれの角周波数における \( \omega C - \frac{1}{\omega L} \) の絶対値を比較すると良いと思います。電流の大きさはこの値の絶対値に依存するからです。
ω₁ = 5 [krad/s]のとき:
→ 横スクロールして下さい →
\[ \begin{aligned} \left|\omega_1 C - \frac{1}{\omega_1 L}\right| &= \left|5 \times 10^3 \times 10 \times 10^{-6} - \frac{1}{5 \times 10^3 \times 1 \times 10^{-3}}\right| \\[10pt] &= \left|5 \times 10^{-2} - \frac{1}{5}\right| \\[10pt] &= \left|0.05 - 0.2\right| \\[10pt] &= |{-0.15}| \\[10pt] &= 0.15 \end{aligned} \]ω₃ = 30 [krad/s]のとき:
→ 横スクロールして下さい →
\[ \begin{aligned} \left|\omega_3 C - \frac{1}{\omega_3 L}\right| &= \left|30 \times 10^3 \times 10 \times 10^{-6} - \frac{1}{30 \times 10^3 \times 1 \times 10^{-3}}\right| \\[10pt] &= \left|30 \times 10^{-2} - \frac{1}{30}\right| \\[10pt] &= \left|0.3 - \frac{1}{30}\right| \\[10pt] &= \left|0.3 - 0.033\right| \\[10pt] &\approx 0.267 \end{aligned} \] <比較すると、\(|\omega_1 C - \frac{1}{\omega_1 L}| = 0.15 < |\omega_3 C - \frac{1}{\omega_3 L}| \approx 0.267\) となります。
したがって、\(I_1 < I_3\)という関係が分かります。
素晴らしい!計算がしっかりできとるな!
まとめると、ω₂ = 10 [krad/s]のときは共振状態で電流I₂が最小になる。そして、ω₁ = 5 [krad/s]とω₃ = 30 [krad/s]のときのリアクタンス成分の絶対値を比較すると、I₁ < I₃となることが分かった。
じゃあ、最終的な3つの電流の大小関係はどうなるんやろか?
→ 横スクロールして下さい →
最終的な3つの電流の大小関係をまとめますと:
1. \(I_2\)が最小:\(\omega_2 = 10\) [krad/s]のとき、回路は共振状態となり、アドミタンスが最小になるため、電流\(I_2\)も最小になります。
2. \(I_1\)と\(I_3\)の比較:計算の結果、\(|\omega_1 C - \frac{1}{\omega_1 L}| = 0.15 < |\omega_3 C - \frac{1}{\omega_3 L}| \approx 0.267\) であることから、\(I_1 < I_3\)となります。
以上から、3つの電流の大小関係は次のようになります:
\(I_2 < I_1 < I_3\)
この関係は選択肢の(3)に対応します。
ほんまによう理解できとるな!完璧や!
結論として、電流の大小関係は I₂ < I₁ < I₃ やから、正解は選択肢の(3)やな!
この問題で大事なポイントは、並列RLC回路では共振状態のときにアドミタンスが最小(つまり電流も最小)になるっていうことと、共振角周波数から離れるほど電流が大きくなるっていうことやな。それと、共振角周波数からどっちに離れるかによって電流の大きさが変わることも大事なポイントやで!
よく頑張ったな!
ありがとうございます!この問題を通して、並列RLC回路の周波数特性について理解が深まりました。
重要なポイントをまとめると:
1. 並列共振回路では、共振角周波数\(\omega_r\)のとき、アドミタンスが最小(インピーダンスが最大)となり、電流も最小になります。これは直列共振回路とは逆の特性です。
2. 共振角周波数は \(\omega_r = \frac{1}{\sqrt{LC}}\) で求められます。
3. 共振点から周波数がずれるほど、\(|\omega C - \frac{1}{\omega L}|\)の値が大きくなり、電流も大きくなります。
4. 共振点よりも高い周波数側と低い周波数側では、同じ周波数差でも電流値が異なります。この問題では高周波側(\(\omega_3\))の方が電流値が大きくなりました。
答えは選択肢の(3)が正解です。
解説まとめ
■ RLC並列回路のアドミタンスとは
RLC並列回路におけるアドミタンスは、回路の「電流通過のしやすさ」を表す量です。抵抗R、インダクタンスL、キャパシタンスCからなる並列回路では、各素子のアドミタンスの和として全体のアドミタンスが求められます。アドミタンスはインピーダンスの逆数であり、その単位はジーメンス[S]です。角周波数によってアドミタンスの値が変化するため、特定の角周波数で共振現象が起こり、回路特性が大きく変わります。
■ 計算手順と公式
- アドミタンスの計算
RLC並列回路のアドミタンスは次式で求められます。
\( \dot{Y} = \frac{1}{R} + j\left(\omega C - \frac{1}{\omega L}\right) \)
ここで、Rは抵抗値[Ω]、Lはインダクタンス[H]、Cはキャパシタンス[F]、ωは角周波数[rad/s]です。
- アドミタンスの大きさの計算
アドミタンスの大きさは次式で計算できます。
\( Y = \sqrt{\left(\frac{1}{R}\right)^2 + \left(\omega C - \frac{1}{\omega L}\right)^2} \)
- 電流の計算
電圧Vが与えられたとき、回路を流れる電流の大きさIは次式で求められます。
\( I = VY \)
- 共振角周波数の計算
アドミタンスが最小(インピーダンスが最大)となる共振角周波数は次式で求められます。
\( \omega_r = \frac{1}{\sqrt{LC}} \)
■ 具体的な計算例
問題条件
- 抵抗値: \( R \)
- インダクタンス: \( L = 1 \times 10^{-3} \ \mathrm{[H]} \)
- キャパシタンス: \( C = 10 \times 10^{-6} \ \mathrm{[F]} \)
- 角周波数: \( \omega_1 = 5 \times 10^{3} \ \mathrm{[rad/s]} \)
- 角周波数: \( \omega_2 = 10^{4} \ \mathrm{[rad/s]} \)
- 角周波数: \( \omega_3 = 30 \times 10^{3} \ \mathrm{[rad/s]} \)
共振角周波数の計算
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{LC}} \\[5pt] &= \frac{1}{\sqrt{1 \times 10^{-3} \times 10 \times 10^{-6}}} \\[5pt] &= \frac{1}{\sqrt{10 \times 10^{-9}}} \\[5pt] &= \frac{1}{\sqrt{10} \times \sqrt{10^{-9}}} \end{aligned} \]ここで、\( \sqrt{10^{-9}} = 10^{-\frac{9}{2}} = 10^{-4.5} \) となります。
したがって:
\[ \begin{aligned} \omega_r &= \frac{1}{\sqrt{10} \times 10^{-4.5}} \\[5pt] &= \frac{10^{4.5}}{\sqrt{10}} \\[5pt] &\approx \frac{10^{4.5}}{3.16} \\[5pt] &\approx 10^4 \ \mathrm{[rad/s]} \end{aligned} \]計算の結果、共振角周波数は \( \omega_r = 10^4 \ \mathrm{[rad/s]} \) となり、これは \( \omega_2 \) に等しいことがわかります。したがって、\( \omega_2 \) のときにアドミタンスは最小となり、電流 \( I_2 \) も最小となります。
各角周波数での虚部の計算
\( \omega_1 \) のときの \( \omega C - \frac{1}{\omega L} \) の絶対値:
→ 横スクロールして下さい →
→ 横スクロールして下さい →
\( \omega_3 \) のときの \( \omega C - \frac{1}{\omega L} \) の絶対値:
\[ \begin{aligned} \left| \omega_3 C - \frac{1}{\omega_3 L} \right| &= \left| 30 \times 10^3 \times 10 \times 10^{-6} - \frac{1}{30 \times 10^3 \times 1 \times 10^{-3}} \right| \\[5pt] &= \left| 0.3 - \frac{1}{30} \right| \\[5pt] &= \left| 0.3 - 0.033 \right| \\[5pt] &\approx 0.267 \end{aligned} \]アドミタンスの虚部の絶対値を比較すると、\( \omega_2 \)(共振角周波数)のときは0、\( \omega_1 \)のときは0.15、\( \omega_3 \)のときは約0.267となります。アドミタンスの大きさは虚部の絶対値が大きいほど大きくなるため、電流値は次の大小関係となります。
結論:\( I_2 < I_1 < I_3 \)である。
■ 実務上の留意点
RLC並列回路のアドミタンス特性と電流特性に関する実務上の留意点です。
- 共振点では回路のインピーダンスが最大(アドミタンスが最小)となり、電流値が最小になります。この特性はバンドストップフィルタなどに利用されます。
- 実際の回路では素子の温度特性や経年変化により、設計上の共振周波数と実際の共振周波数にずれが生じることがあります。
- 高Q値の共振回路では、共振点付近での特性変化が急峻になるため、周波数選択性は高まりますが、温度変化などの影響も受けやすくなります。
- 電力系統では、高調波フィルタとして並列共振回路が使用され、特定の周波数成分を選択的に吸収します。
- 通信機器やアンテナ整合回路などでは、RLC並列回路の周波数特性を利用して帯域制限や整合を行います。
- 共振点を外れた状態では、低周波側ではインダクタンス成分が支配的、高周波側ではキャパシタンス成分が支配的になる特性があります。