【機械】令和6年 (下期) 問4|三相誘導電動機の損失計算および二次銅損の算出に関する計算問題
電源に接続された三相誘導電動機が駆動されている。
電源の線間電圧 \( V_{\mathrm{n}} \) は \( 400 \) [V],電源から供給される線電流 \( I_{l} \) は \( 25.8 \) [A],力率は \( 0.8 \) である。
この場合の滑り \( s \) が \( 4 \) [%] であり,鉄損 \( P_{\mathrm{i}} \) 及び一次銅損 \( P_{\mathrm{c1}} \) の値は,共に,二次銅損 \( P_{\mathrm{c2}} \) の値の \( \displaystyle \frac{1}{2} \) である。
この場合の二次銅損 \( P_{\mathrm{c2}} \) の値 [W] として最も近いものを次の (1)~(5) のうちから一つ選べ。
合格への方程式
誘導電動機の基本原理
三相誘導電動機って何?
三相誘導電動機は、工場やビルで最もよく使われているモーターです。コンセントから電気を流すだけで回転する、とても便利な機械なんです。
誘導電動機の特徴
• ブラシがない(メンテナンスが楽!)
• 構造がシンプル(壊れにくい!)
• 回転磁界で動く(磁石がくるくる回るイメージ)
同期速度と実際の回転速度
誘導電動機には「同期速度」という理論上の速度があります。これは回転磁界が回る速度のことで、実際のモーターは少し遅れて回ります。
身近な例え
メリーゴーラウンドの外側を走りながら、中の馬を追いかけるイメージです。馬(回転子)は外を走る人(回転磁界)より少し遅れて動きます。
同期速度の計算式
\[ N_{\mathrm{s}} = \frac{120f}{p} \quad \mathrm{[min^{-1}]} \]ここで:
• ( N_{\mathrm{s}} ):同期速度(1分間の回転数)
• ( f ):電源周波数 [Hz](東日本50Hz、西日本60Hz)
• ( p ):極数(磁石の数みたいなもの)
覚え方のコツ
「120」という数字は、60秒×2(N極とS極)から来ています。周波数50Hzで2極なら、120×50÷2=3000回転/分になります。
同期角速度(ちょっと発展)
\[ \omega_{\mathrm{s}} = \frac{2\pi f}{p} \quad \mathrm{[rad/s]} \]角速度は「1秒間に何ラジアン回るか」を表します。機械系の計算でよく使います。
なぜ「誘導」電動機と呼ぶの?
回転子に電流が「誘導」されて(勝手に流れて)動くからです。永久磁石を使わず、電磁誘導の原理で動くのが特徴です。
| 電動機の種類 | 動作原理 | 特徴 |
|---|---|---|
| 誘導電動機 | 電磁誘導 | 構造が簡単、丈夫 |
| 同期電動機 | 磁石の吸引力 | 効率が高い、制御が複雑 |
| 直流電動機 | フレミングの法則 | 速度制御が簡単、ブラシ必要 |
等価回路と損失の理解
L形等価回路を理解しよう
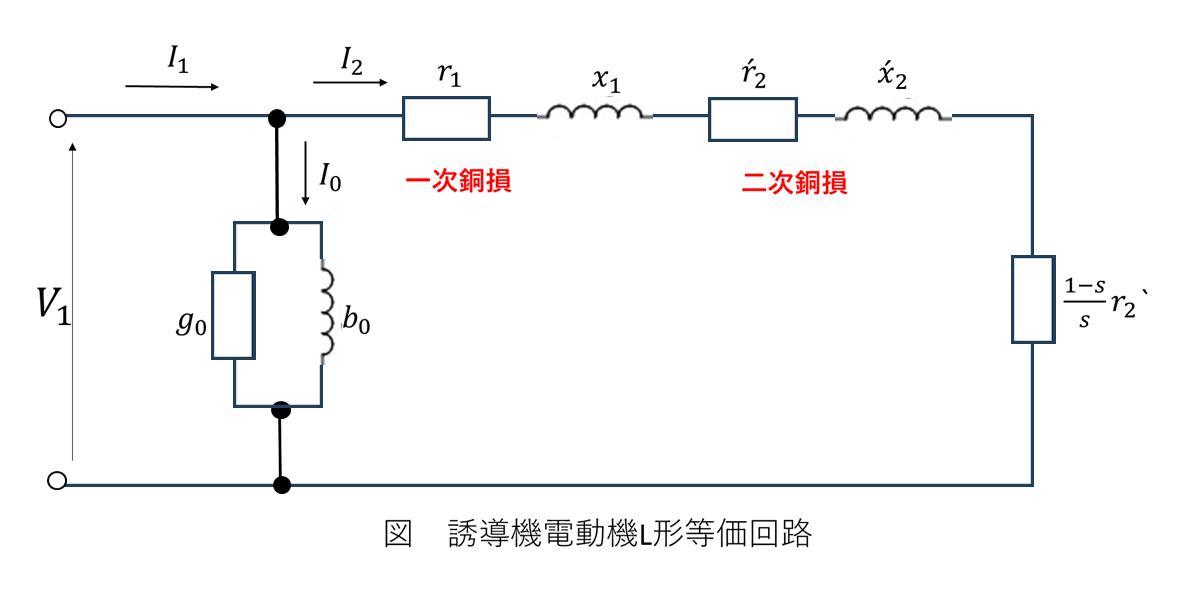
この回路図は、誘導電動機の内部で起きていることを電気回路で表現したものです。実際のモーターを分解しても、こんな部品は見えませんが、電気的にはこのように考えることができます。
回路の各部品の意味
•\( r_1 \):一次巻線抵抗(固定子の電線の抵抗)
• \( x_1 \):一次漏れリアクタンス(漏れ磁束による)
• \( r_2' \):二次抵抗の一次換算値(回転子の抵抗)
•\( x_2' \):二次漏れリアクタンスの一次換算値
• \( \frac{1-s}{s}r_2' \):機械的出力を表す抵抗
誘導電動機の損失を整理しよう
電動機に入力された電力は、すべてが有効な仕事(回転力)になるわけではありません。途中でいろんな損失が発生します。
損失の流れ(イメージ)
入力電力 → 鉄損 ↓
→ 一次銅損 ↓
→ 二次銅損 ↓
→ 機械出力
各損失の特徴
• 鉄損:磁束による損失(ほぼ一定)
• 一次銅損:固定子巻線の抵抗損
• 二次銅損:回転子の抵抗損(滑りに比例)
損失の計算式をチェック
| 損失の種類 | 計算式 | 特徴 |
|---|---|---|
| 鉄損 \( P_{\mathrm{i}} \) | ほぼ一定値 | 電圧に依存、負荷によらない |
| 一次銅損 \( P_{\mathrm{c1}} \) | \( 3r_1{I_1}^2 \) | 一次電流の2乗に比例 |
| 二次銅損 \( P_{\mathrm{c2}} \) | \( 3r_2'{I_2'}^2 \) | 滑りに比例、負荷で変化 |
注意点
等価回路では、機械的出力が抵抗 ( \frac{1-s}{s}r_2' ) で表現されます。これは実際の抵抗ではなく、機械的パワーを電気的に表現したものです。
電力の流れを追いかけよう
\[ \begin{aligned} \text{一次入力} \, P_1 &= \sqrt{3}V_{\mathrm{n}}I_l\cos\theta \\[10pt] \text{二次入力} \, P_2 &= P_1 - P_{\mathrm{i}} - P_{\mathrm{c1}} \\[10pt] \text{機械出力} \, P_{\mathrm{o}} &= P_2 - P_{\mathrm{c2}} \end{aligned} \]この関係を理解すれば、どの損失からでも他の値を計算できるようになります。
滑りと出力の関係
滑り(スリップ)って何?
滑り ( s ) は、誘導電動機の最重要パラメータです。同期速度と実際の回転速度の差を表します。
\[ s = \frac{N_{\mathrm{s}} - N}{N_{\mathrm{s}}} \]身近な例え
エスカレーターの手すりと階段の速度差をイメージしてください。手すり(同期速度)より階段(実際の回転)が少し遅れるのが滑りです。
滑りの特徴
| 運転状態 | 滑りの値 | 説明 |
|---|---|---|
| 始動時 | s = 1 (100%) | 回転子は止まっている |
| 通常運転 | s = 0.02~0.05 | 2~5%程度の滑り |
| 無負荷 | s ≈ 0 | ほぼ同期速度で回転 |
滑りと電力の黄金比
これは電験三種で超重要な関係式です!
二次側の電力配分の法則
\[ P_2 : P_{\mathrm{o}} : P_{\mathrm{c2}} = 1 : (1-s) : s \]つまり、二次入力を1とすると:
• 機械出力は (1-s) の割合
• 二次銅損は s の割合
なぜこの関係が成り立つの?
等価回路を見ると、二次側の抵抗が ( \frac{r_2'}{s} ) と表されます。これを分解すると:
\[ \frac{r_2'}{s} = r_2' + \frac{1-s}{s}r_2' \]• 第1項 ( r_2' ):二次銅損を生む抵抗
• 第2項 ( \frac{1-s}{s}r_2' ):機械出力を表す仮想抵抗
計算のコツ
滑りが4%なら、二次入力の96%が機械出力、4%が二次銅損になります。この比率を使えば、一つの値から他の値を簡単に求められます。
実際の計算で使う関係式
\[ \begin{aligned} P_{\mathrm{o}} &= \frac{1-s}{s} \times P_{\mathrm{c2}} \\[10pt] P_{\mathrm{c2}} &= s \times P_2 \\[10pt] P_{\mathrm{o}} &= (1-s) \times P_2 \end{aligned} \]よくある間違い
滑りを%で計算するときは、必ず小数に直してから使いましょう。4%なら0.04として計算します。
計算テクニック
電験三種でよく出る計算パターン
誘導電動機の問題では、与えられた条件から順番に値を求めていくのがポイントです。
1. 一次入力の計算
三相交流の電力計算は基本中の基本!
\[ P_1 = \sqrt{3} \times V_{\mathrm{n}} \times I_l \times \cos\theta \]覚え方
「ルート3(1.732)× 線間電圧 × 線電流 × 力率」
単相なら√3は不要です。
2. 効率の計算
\[ \eta = \frac{P_{\mathrm{o}}}{P_1} \times 100 \, [\%] \]また、損失から計算する場合:
\[ \eta = \frac{P_{\mathrm{o}}}{P_{\mathrm{o}} + P_{\mathrm{i}} + P_{\mathrm{c1}} + P_{\mathrm{c2}}} \times 100 \]問題を解く手順
基本的な解法の流れ
1. 与えられた条件を整理する
2. 一次入力 ( P_1 ) を計算
3. 滑りと電力の関係式を活用
4. 損失の関係(問題文の条件)を式に
5. 連立方程式を解く
計算を楽にするテクニック
| テクニック | 内容 |
|---|---|
| 単位に注意 | kW と W を混同しない |
| 有効数字 | 選択肢を見て必要な桁数を判断 |
| 検算方法 | 効率が0~100%の範囲か確認 |
| 比の活用 | 滑りの比率で素早く計算 |
実戦的なアドバイス
問題文の読み方
• 「共に」「それぞれ」などの表現に注意
• 損失の関係が「○倍」か「○分の1」か確認
• 与えられた値の単位を必ずチェック
よく出る損失の関係パターン
問題では以下のような条件がよく出ます:
- 「鉄損と一次銅損が等しい」
- 「各損失が二次銅損の○倍」
- 「全損失が出力の○%」
最終チェック
• 出力 < 入力 になっているか
• 滑りが通常範囲(2~5%程度)か
• 選択肢の中から最も近い値を選ぶ
まとめ:重要公式集
絶対覚える公式
\[ \begin{aligned} &\text{1. } P_2 : P_{\mathrm{o}} : P_{\mathrm{c2}} = 1 : (1-s) : s \\[10pt] &\text{2. } P_1 = \sqrt{3}V_{\mathrm{n}}I_l\cos\theta \\[10pt] &\text{3. } s = \frac{N_{\mathrm{s}} - N}{N_{\mathrm{s}}} \\[10pt] &\text{4. } N_{\mathrm{s}} = \frac{120f}{p} \end{aligned} \]🔍 ワンポイントアドバイス:誘導電動機の問題では「滑りと電力の比(1:(1-s):s)」が最重要!この関係さえ覚えていれば、多くの問題が解けます。また、L形等価回路の ( \frac{1-s}{s}r_2' ) は機械出力を表す仮想抵抗だということを理解しておけば、回路の意味がスッキリ分かりますよ。電験三種では滑り4%前後の問題が多いので、この値で練習しておくと本番で役立ちます!
今日は三相誘導電動機の損失計算について勉強していこか!まず問題文を一緒に見てみよう。電源に接続された三相誘導電動機があって、線間電圧が400V、線電流が25.8A、力率が0.8やねん。で、滑りが4%で、鉄損と一次銅損が両方とも二次銅損の半分になってるって条件や。この問題、最近の電験三種では珍しいパターンやから、しっかり理解していこな!まず、誘導電動機って何か知ってる?
誘導電動機は、回転磁界によって回転子に誘導電流が流れて、その電流と磁界の相互作用でトルクが発生する電動機ですね。三相交流を固定子巻線に流すと回転磁界ができて、それに回転子が「ついていこう」とする感じで回転します。
身近な例では、エアコンのコンプレッサーや工場のベルトコンベア、エレベーターなどに使われています。構造が簡単で丈夫なので、産業界では最も多く使われている電動機です!
そうそう!誘導電動機は産業界の主役やな。ところで、この問題で重要な「滑り」って概念、ちゃんと理解してる?滑りが4%って書いてあるけど、これが何を意味するか説明してみて。
滑り \( s \) は、同期速度と実際の回転速度の差を表す重要な概念です。式で表すと:
\[ \begin{aligned} s &= \frac{N_s - N}{N_s} \\[10pt] &= \frac{\text{同期速度} - \text{実際の回転速度}}{\text{同期速度}} \end{aligned} \]滑り4%ということは、回転子が同期速度の96%の速度で回転しているということです。例えば、同期速度が1500rpmなら、実際は1440rpmで回転していることになります。
なぜ「滑り」と呼ぶかというと、回転子が回転磁界に対して少し「滑って」遅れているイメージだからです。この滑りがないと誘導電流が発生せず、トルクも生まれません!
ええ感じやな!滑りの理解はバッチリや。じゃあ次は、問題を解くために必要な一次入力 \( P_1 \) を計算してみよか。線間電圧400V、線電流25.8A、力率0.8から三相電力の公式使うんやけど、覚えてる?
三相電力の公式を使います!三相交流の有効電力は:
\[ \begin{aligned} P_1 &= \sqrt{3} \times V_n \times I_l \times \cos\theta \\[10pt] &= \sqrt{3} \times 400 \times 25.8 \times 0.8 \end{aligned} \]計算してみます:
\[ \begin{aligned} P_1 &= 1.732 \times 400 \times 25.8 \times 0.8 \\[10pt] &= 1.732 \times 8256 \\[10pt] &≒ 14,300 \, \mathrm{[W]} \end{aligned} \]この \( \sqrt{3} \) が出てくるのは、三相交流の線間電圧と相電圧の関係から来ています。Y結線では線間電圧が相電圧の \( \sqrt{3} \) 倍になるんですよね!
完璧や!14.3kWの電力が入力されてるわけやな。ところで、誘導電動機の中でこの電力がどう使われるか知ってる?実は、誘導電動機にはL形等価回路っていう便利な表現方法があるんや。
この回路、どう見たらええか分かる?
L形等価回路は誘導電動機を電気回路として表現したものですね!各要素の意味を説明します:
・\( r_1 \):一次巻線抵抗(固定子の銅線の抵抗)
・\( x_1 \):一次漏れリアクタンス(固定子の漏れ磁束による)
・\( r_2'/s \):二次側の等価抵抗(回転子側を一次側に換算)
・\( x_2' \):二次漏れリアクタンス(回転子の漏れ磁束による)
特に重要なのは \( r_2'/s \) の部分で、これを \( r_2' + r_2'(1-s)/s \) と分解すると:
・\( r_2' \):二次銅損を表す抵抗
・\( r_2'(1-s)/s \):機械的出力を表す等価抵抗
つまり、電気的な損失と機械的な出力を抵抗として表現しているんです!すごく便利な考え方ですね。
その通りや!L形等価回路はホンマに便利やねん。ここで超重要なポイントがあるんや。二次入力 \( P_2 \)、出力 \( P_o \)、二次銅損 \( P_{c2} \) の間には、めっちゃキレイな比例関係があるねん。これ、電験三種では必須の知識やで!どんな関係か予想できる?
これは誘導電動機の重要な性質ですね!L形等価回路から導かれる関係式は:
\[ \begin{aligned} P_2 : P_o : P_{c2} = 1 : (1-s) : s \end{aligned} \]つまり、滑りが4%(s = 0.04)の場合:
・二次入力を100とすると
・機械的出力は96(100×0.96)
・二次銅損は4(100×0.04)
この関係を覚えるコツは「滑った分だけ損失になる」というイメージです。滑りが大きいほど二次銅損が増えて、効率が悪くなるんです。だから誘導電動機は滑りを小さくして運転するのが基本なんですね!
素晴らしい理解や!「滑った分だけ損失」って覚え方、ええな〜。じゃあ、この関係式を使って、出力 \( P_o \) を二次銅損 \( P_{c2} \) で表してみて。滑り4%やから計算も楽やで!
比例関係から出力を二次銅損で表します:
\[ \begin{aligned} \frac{P_o}{P_{c2}} &= \frac{1-s}{s} \\[10pt] P_o &= \frac{1-s}{s} \times P_{c2} \\[10pt] &= \frac{1-0.04}{0.04} \times P_{c2} \\[10pt] &= \frac{0.96}{0.04} \times P_{c2} \\[10pt] &= 24 \times P_{c2} \end{aligned} \]つまり、出力は二次銅損の24倍になります!滑りが小さいほど、この倍率は大きくなるんです。例えば滑り2%なら49倍、1%なら99倍にもなります。これが誘導電動機の効率が良い理由の一つですね。
ええ感じで理解してるな!さて、ここからが今回の問題のポイントや。問題文には「鉄損と一次銅損が両方とも二次銅損の半分」って書いてある。これを式で表すとどうなる?
問題文の条件を式で表すと:
\( P_i = \frac{1}{2} P_{c2} \)(鉄損は二次銅損の半分)
\( P_{c1} = \frac{1}{2} P_{c2} \)(一次銅損も二次銅損の半分)
これは珍しい条件設定ですね。通常、鉄損は負荷によらず一定で、銅損は負荷の2乗に比例するので、こういう関係になることは実際には稀です。でも、試験問題としては計算を簡単にするための設定だと理解できます。
ちなみに、実際の誘導電動機では定格運転時に全損失の30〜40%が鉄損、60〜70%が銅損(一次と二次の合計)になることが多いです!
そうそう、実際とは違う設定やけど、計算問題としては面白いな。さあ、いよいよ最後の計算や!一次入力 \( P_1 = 14,300 \) Wは、出力と全部の損失の合計になるはずやな。これを式にして、二次銅損 \( P_{c2} \) を求めてみよか!
一次入力は出力と全損失の合計なので:
\[ \begin{aligned} P_1 &= P_o + P_i + P_{c1} + P_{c2} \\[10pt] &= 24P_{c2} + \frac{1}{2}P_{c2} + \frac{1}{2}P_{c2} + P_{c2} \end{aligned} \]ちょっと待って、計算を整理してみます:
\[ \begin{aligned} P_1 &= P_{c2}(24 + \frac{1}{2} + \frac{1}{2} + 1) \\[10pt] &= P_{c2}(24 + 0.5 + 0.5 + 1) \\[10pt] &= P_{c2} \times 26 \end{aligned} \]あ、すみません!さっき出力の計算で間違えました。正しくは:
\[ \begin{aligned} P_o &= \frac{1-0.04}{0.04} \times P_{c2} = \frac{0.96}{0.04} \times P_{c2} = 24P_{c2} \end{aligned} \]これで合ってますね。続けて計算すると:
\[ \begin{aligned} 14,300 &= 26 \times P_{c2} \\[10pt] P_{c2} &= \frac{14,300}{26} \\[10pt] &= 550 \, \mathrm{[W]} \end{aligned} \]完璧や!答えは550Wで選択肢(3)やな。ところで、この問題から学べることをまとめてみよか。誘導電動機の損失と効率について、どんなことが重要やと思う?
この問題から学んだ重要ポイントをまとめます:
1. 滑りと損失の関係
\( P_2 : P_o : P_{c2} = 1 : (1-s) : s \) という黄金比は必ず覚えておくべきです。これは誘導機の基本中の基本!
2. 損失の種類と発生場所
・鉄損:固定子鉄心で発生(ヒステリシス損+渦電流損)
・一次銅損:固定子巻線の抵抗による損失
・二次銅損:回転子巻線(または導体)の抵抗による損失
3. 効率向上のポイント
・滑りを小さくする(二次銅損を減らす)
・高品質な電磁鋼板を使う(鉄損を減らす)
・太い導体を使う(銅損を減らす)
4. 実務での応用
実際の現場では、誘導電動機の効率は80〜95%程度。大型になるほど効率が良くなります。省エネのためには高効率モータ(プレミアム効率モータ)の採用が重要です!
最後に、類似問題への対策も考えとこか。もし「滑りが2%」やったら、二次銅損はどうなると思う?計算の流れは同じやから、チャレンジしてみて!
滑りが2%(s = 0.02)の場合を計算してみます!
まず、出力と二次銅損の関係:
\[ \begin{aligned} P_o &= \frac{1-s}{s} \times P_{c2} \\[10pt] &= \frac{1-0.02}{0.02} \times P_{c2} \\[10pt] &= \frac{0.98}{0.02} \times P_{c2} \\[10pt] &= 49 \times P_{c2} \end{aligned} \]一次入力の式は:
\[ \begin{aligned} P_1 &= P_o + P_i + P_{c1} + P_{c2} \\[10pt] 14,300 &= 49P_{c2} + \frac{1}{2}P_{c2} + \frac{1}{2}P_{c2} + P_{c2} \\[10pt] 14,300 &= 51P_{c2} \\[10pt] P_{c2} &= \frac{14,300}{51} ≒ 280 \, \mathrm{[W]} \end{aligned} \]滑りが半分(4%→2%)になると、二次銅損も約半分(550W→280W)になりました!これは滑りと二次銅損が比例関係にあることを示しています。効率も良くなりますね!
素晴らしい!滑りと二次銅損の関係がよく分かったな。最後にもう一つ、実務で役立つ豆知識を教えたろか。誘導電動機の滑りって、実は簡単に測定できるんやで。どうやると思う?
実務での滑り測定方法をご紹介します!
1. ストロボスコープ法
回転子にマークを付けて、電源周波数に同期したストロボ光を当てます。マークがゆっくり動いて見える速度から滑りを計算できます。
2. 回転計による直接測定
非接触式回転計で実際の回転速度を測り、同期速度との差から計算します。
例:4極50Hzなら同期速度1500rpm、実測1440rpmなら滑り4%
3. 電流波形解析法
固定子電流に含まれる回転子スロット高調波を解析して滑りを推定します。最新の診断技術です!
覚えておくと便利な公式
同期速度 \( N_s = \frac{120f}{p} \) [rpm]
(f:周波数[Hz]、p:極数)
これで電験三種の誘導電動機問題は怖くないですね!頑張って合格目指しましょう!
解説まとめ
■ 三相誘導電動機の損失と出力の関係とは
三相誘導電動機において、電源から供給された電力(一次入力)は、各種損失を経て機械的出力に変換されます。主な損失には鉄損、一次銅損、二次銅損があり、これらの関係を理解することで、与えられた条件から各損失を計算できます。特に重要なのは、二次入力・出力・二次銅損の間には滑りsを用いた比例関係があることです。
■ 計算手順と公式
- 一次入力の計算
三相交流電源から供給される電力を計算します。
\( P_1 = \sqrt{3} V_n I_l \cos\theta \)
- 滑りと損失の関係式の理解
誘導電動機の二次側では、以下の重要な関係が成立します。
\( P_2 : P_o : P_{c2} = 1 : (1-s) : s \)
- 出力と二次銅損の関係
上記の関係から、出力は二次銅損を用いて表現できます。
\( P_o = \frac{1-s}{s} P_{c2} \)
- 全損失を考慮した一次入力の式
一次入力は出力と全損失の和となります。
\( P_1 = P_o + P_i + P_{c1} + P_{c2} \)
■ 具体的な計算例
問題条件
- 線間電圧:\( V_n = 400 \) V
- 線電流:\( I_l = 25.8 \) A
- 力率:\( \cos\theta = 0.8 \)
- 滑り:\( s = 0.04 \) (4%)
- 鉄損と一次銅損:それぞれ二次銅損の1/2
一次入力の計算
\[ \begin{aligned} P_1 &= \sqrt{3} V_n I_l \cos\theta \\[5pt] &= \sqrt{3} \times 400 \times 25.8 \times 0.8 \\[5pt] &\approx 14300 \ \mathrm{[W]} \end{aligned} \]出力と損失の関係式の導出
出力を二次銅損で表現すると:
\[ P_o = \frac{1-s}{s} P_{c2} = \frac{1-0.04}{0.04} P_{c2} = \frac{0.96}{0.04} P_{c2} = 24 P_{c2} \]また、問題条件より:
\[ \begin{aligned} P_i &= \frac{1}{2} P_{c2} \\[5pt] P_{c1} &= \frac{1}{2} P_{c2} \end{aligned} \]一次入力の式に代入
\[ \begin{aligned} P_1 &= P_o + P_i + P_{c1} + P_{c2} \\[5pt] &= 24P_{c2} + \frac{1}{2}P_{c2} + \frac{1}{2}P_{c2} + P_{c2} \\[5pt] &= \left(24 + \frac{1}{2} + \frac{1}{2} + 1\right) P_{c2} \\[5pt] &= 26 P_{c2} \end{aligned} \]二次銅損の計算
\[ \begin{aligned} 14300 &= 26 P_{c2} \\[5pt] P_{c2} &= \frac{14300}{26} \\[5pt] &= 550 \ \mathrm{[W]} \end{aligned} \]結論:二次銅損は 550 W となり、選択肢 (3) が正解です。
■ 実務上の留意点
誘導電動機の効率改善や保守管理において、各種損失の把握は重要です。特に以下の点に注意が必要です。
- 滑りが大きくなると二次銅損が増加し、効率が低下します。定格運転時の滑りは通常2~5%程度です。
- 二次銅損は回転子の発熱の主要因となるため、適切な冷却が必要です。
- L形等価回路を用いることで、複雑な誘導機の特性を簡潔に解析できます。
- 実際の設計では、損失を最小化するために、巻線抵抗の低減や磁気回路の最適化が行われます。